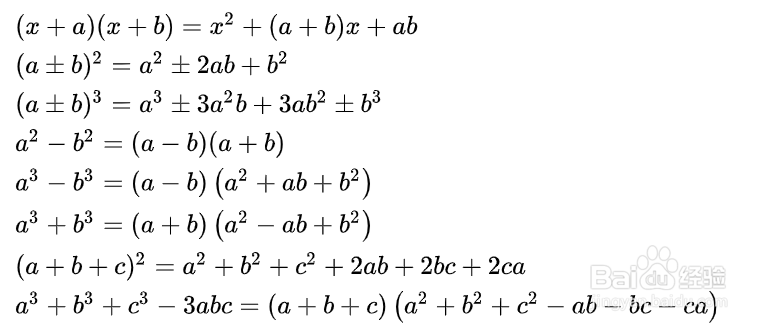1、第一:找准公因式,一次要提净;全家都搬走,留1把家守。要变号,变形看正负。例如:-am+bm+cm=-m(a-b-c);a(x-y)+b(y-x)=a(x-y)-b(x-y)=(x-y)(a-b)。
2、第二:如果把乘法公式反过来,就可以把某些多项式分解因式,这种方法叫公式法。平方差公式:a2-b2=(a+b)(a-b);完全平方公式:a2±2ab+b2=(a±b)2;
3、第三:将ax2+bx+c(a,b,c是常数,ab≠0)因式分解,可令ax2+bx+c=0,聪艄料姹再解这个方程。如果方程无解,则原式无法因式分解;如果方程有两个相同的实数根(设为m),则原式可以分鞅瓞慈玢解为(x-m)2如果方程有两个不相等的实数根(分别设为m,n),则原式可以分解为(x-m)(x-n)。
4、第四:十字分解法的方法简单来讲就是:十字左边相乘等于二次项系数,右边相乘等于常数项,交叉相乘再相加等于一次项系数。其实就是运用乘法公式(x+a)(x+b)=x²+(a+b)x+ab的逆运算来进行因式分解。