1、 先明白什么是质数/素数素数又称为质数,一个大于1的自然数,除了1和它自身外,不能被其他自然数整除的数叫做质数
2、 编程实现:判断一个数是否为质数/素数明白了什么是质数/素数后,我们就要思考如何编程实现其核心算法最简单的是遍历法: 即遍历1到其本身,如果除了1和它本身外(2 - n-1),如果每个数都不能被他整除的话,那么就说明这个数是素数int i, n=7, flag = 0;for (i = 2; i < n; i++){if (n % i == 0){flag++;}}if (flag == 0){printf("%d是质数/素数", n);//表示是素数}else{printf("%d不是质数/素数", n);//表示不是素数}
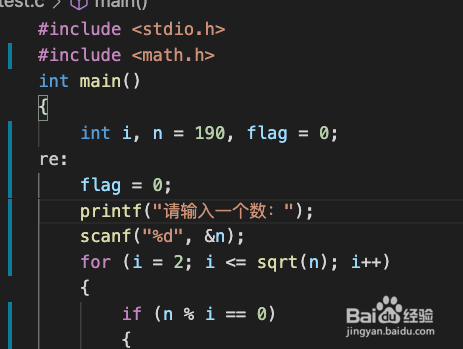
3、 完整可运行代码#include <stdio.h>int main(){int i, n=7, flag = 0;for (i = 2; i < n; i++){if (n % i == 0){flag++;}}if (flag == 0){printf("%d是质数/素数", n);//表示是素数}else{printf("%d不是质数/素数", n);//表示不是素数}printf("\n");return 0;}
4、 程序执行结果请输入一个数:55是质数/素数请输入一个数:1515不是质数/素数请输入一个数:1919是质数/素数请输入一个数:2020不是质数/素数
5、 逻辑优化对一个判读一个数m,上面我们遍历时是直接判断到m-1的,其实判断方法还可以简化。m 不必被 2 ~ m-1 之间的每一个整数去除,只需被 2 ~ sqrt(m) 之间的每一个整数去除就可以了。如果 m 不能被 2 ~ 间任一整数整除,m 必定是素数。例如判别 17 是是否为素数,只需使 17 被 2~4 之间的每一个整数去除,由于都不能整除,可以判定 17 是素数。 原因:因为如果 m 能被 2 ~ m-1 之间任一整数整除,其二个因子必定有一个小于或等于sqrt(m) ,另一个大于或等于sqrt(m) 。例如 16 能被 2、4、8 整除,16=2*8,2 小于 4,8 大于 4,16=4*4,4=sqrt(16),因此只需判定在 2~4 之间有无因子即可。代码调整: #include <math.h> //先引入库文件 for (i = 2; i < n; i++) //然后这里i < n 可以改成i<=sqrt(n)
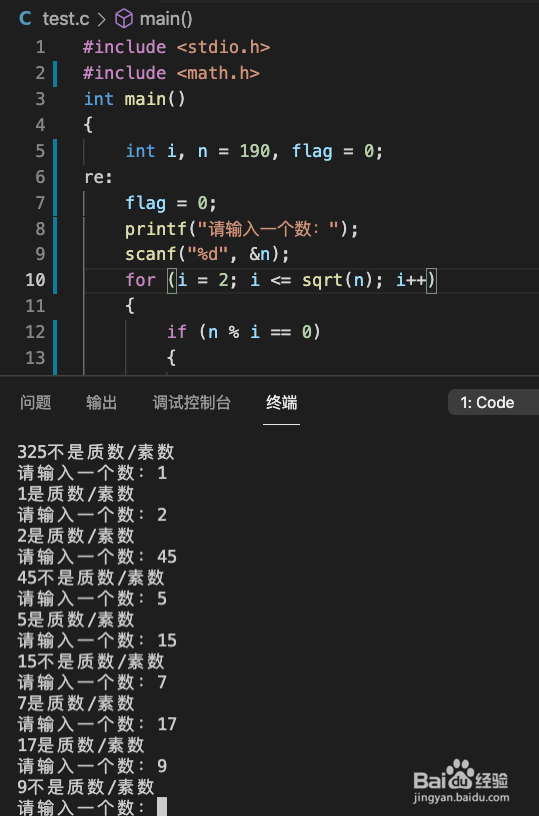
6、 优化后的执行结果仍然无误请输入一个数:22是质数/素数请输入一个数:4545不是质数/素数请输入一个数:55是质数/素数请输入一个数:1515不是质数/素数请输入一个数:77是质数/素数请输入一个数:1717是质数/素数请输入一个数:99不是质数/素数
7、 最后我们扩展下:求101到200之间的素数#include <stdio.h>#include <stdlib.h>#include <string.h>/*判断101到200之间的素数 素数:“素数是指质数,一个大于1的自然数,除了1和它自身外,不能整除其他自然数的数叫做质数;否则称为合数 思路1):因此判断一个整数m是否是素数,只需把 m 被 2 ~ m-1 之间的每一个整数去除,如果都不能被整除,那么 m 就是一个素数。 思路2):另外判断方法还可以简化。m 不必被 2 ~ m-1 之间的每一个整数去除,只需被 2 ~ sqrt(m) 之间的每一个整数去除就可以了。如果 m 不能被 2 ~ 间任一整数整除,m 必定是素数。例如判别 17 是是否为素数,只需使 17 被 2~4 之间的每一个整数去除,由于都不能整除,可以判定 17 是素数。 原因:因为如果 m 能被 2 ~ m-1 之间任一整数整除,其二个因子必定有一个小于或等于sqrt(m) ,另一个大于或等于sqrt(m) 。例如 16 能被 2、4、8 整除,16=2*8,2 小于 4,8 大于 4,16=4*4,4=sqrt(16),因此只需判定在 2~4 之间有无因子即可。 */void main(){int n,i,j,flag=0,sum=0;printf("素数:");for(i=101;i<=200;i++){flag=0;for(j=2;j<i;j++){ //这里j<i可以改成<=sqrt(i)if(i%j==0) {flag=1;}}if(flag==0){sum++; //表示是素数printf("%d,",i);}}printf("\n共有素数%d个\n",sum);}
8、求101到200之间的素数/质数执行结果素数:101,103,107,109,113,127,131,137,139,149,151,157,163,167,173,179,181,191,193,197,199,共有素数21个