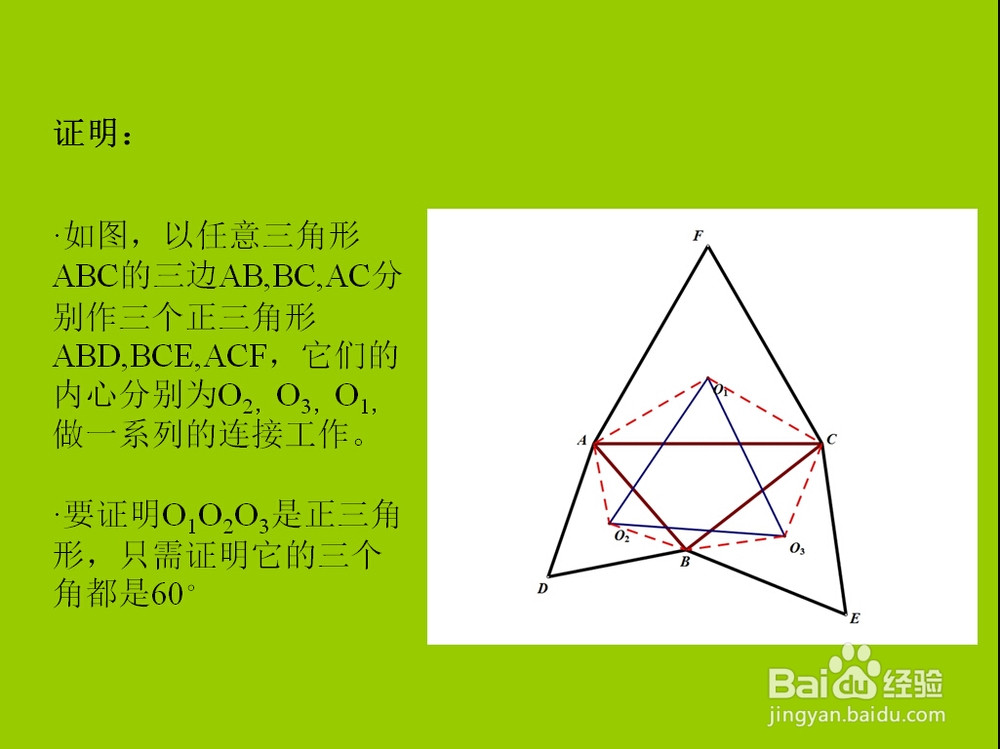
1、·如图,以任意三角形ABC的三边AB,BC,AC分别作三个正三角形ABD,BCE,ACF,它们的内心分别为O2,O3,O1,做一系列的连接工作。·要证明O1O2O3是正三角形,只需证明它的三个角都是60°
2、∵△ACF是正三角形∴∠AO1C为120°同理可证,另外两个角∠AO2B和∠BO3C也都是120°.于是,在六边形AO2BO3CO1中,剩下的三个角的和是360°.所以,这三个三角形△AO2B,△O2BO3,△O3CO1就能拼凑为一个与△O1O2O3全等的三角形。如何拼凑请看下一步
3、如图,可以想象把三角形像折纸一样向三角形△O1O2O3内部翻折,把它们拼凑在一起。于是∠AO1O2+∠CO1O3=∠O2O1O3而∠AO1C=∠AO1O2+∠CO1O泌驾台佐3+∠O2O1O3=2·∠O2O1O3 =120°所以得出∠O2O1O3=60°同理,∠O1O2O3=∠O2O3O1=60°∴△O1O2O3乃正三角形是也。