1、※.函数的定义域∵√x有x≥0;对12/x有x≠0.∴函数的定义域为:(0,+∞)。
2、∵y=√x(85x+12/x)=85x^(3/2)+12x^(-1/2),对x求导得:∴dy/dx=(3/2)*85x^(1/2)-(12/2)x^(-3/2)=(1/2)x^(-3/2)(3忮氽阝另*85x²-12).令dy/dx=0,则x²=4/85.又因为x>0,则x=(2/85)√85≈0.22.(1)当x∈(0, (2/85)√85)时,dy/dx<0,函数y为单调减函数;(2)当x∈[(2/85)√85,+∞)时,dy/dx>0,函数y为单调增函数。
3、∵dy/dx=(1/2)x^(-3/2)(3涯箨唁峦*85x²-12),∴d^2y/dx^2=-3/4*x^(-5/2)(3*85x²-12)+3*85x*x^(-3/2)=-3/4*x^(幻腾寂埒-5/2)(3*85x²-12)+3*85x^(-1/2)=-3/4x^(-5/2)(3*85x²-12-4*85x²)=3/4x^(-5/2)(85x²+12)>0,则:函数y在定义域上为凹函数。
4、※.函数的极限Lim(x→0) √x(85x+12/x)=+∞Lim(x→+∞) √x(85x+12/x)=+∞。
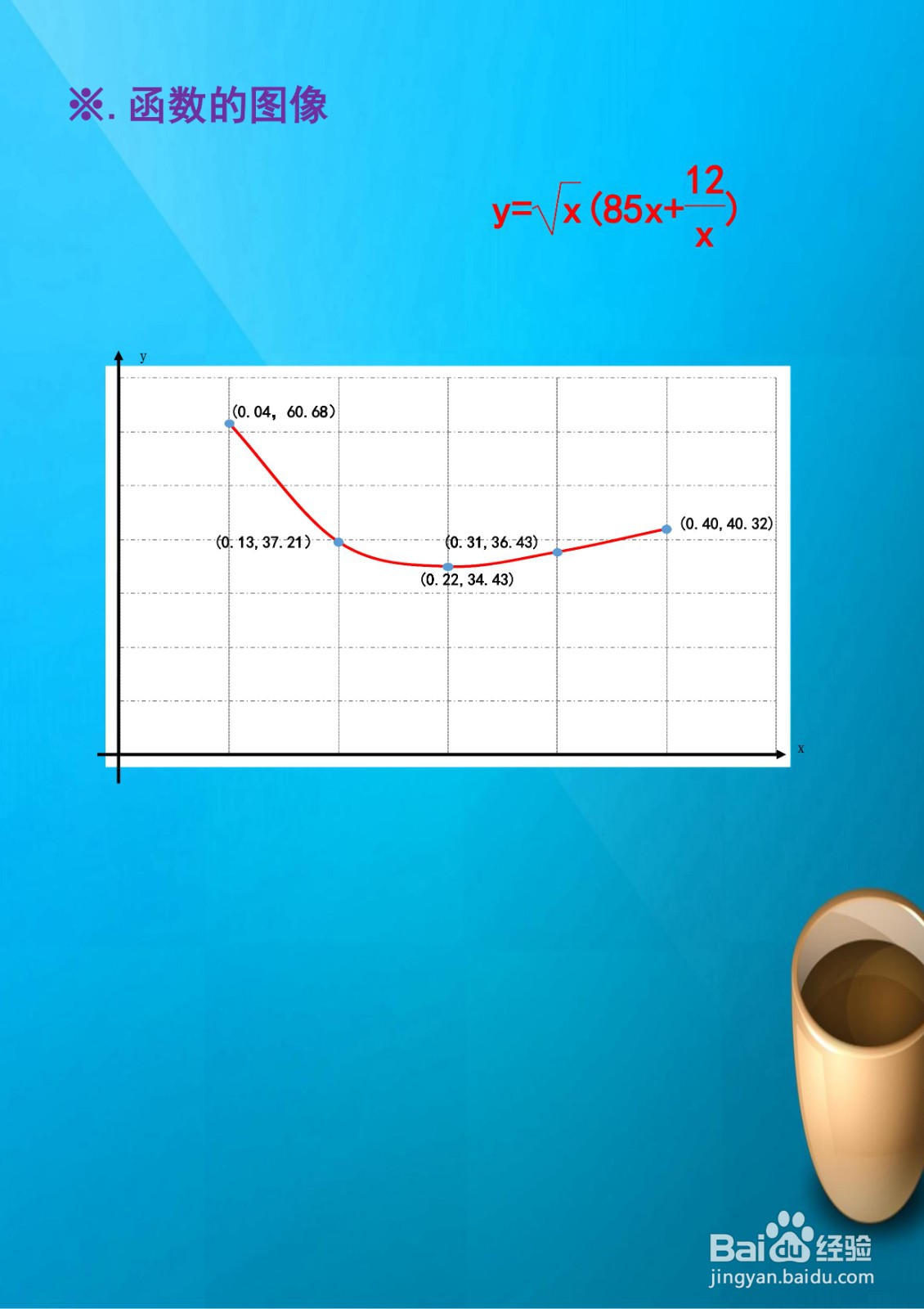
5、综合以上函数的定义域、单调性、凸凹性等性质,解析函数的图像示意图如下。