源自于洛家弟子安卓于2019年5月13日的提问:走马灯数与洛书有没有什么对应或则对应的原理?跟洛书数理有什么不一样吗?走马灯数,即一个六位数字:142857,在很久前我便关注到这个数字的存在,但一直没想着花心思去思考它所涉及的一些数理规律。考虑到这件事情本身有助于弘扬洛家的探索精神,所以便有此一试。
工具/原料
走马灯数142857
洛书
走马灯数的规律
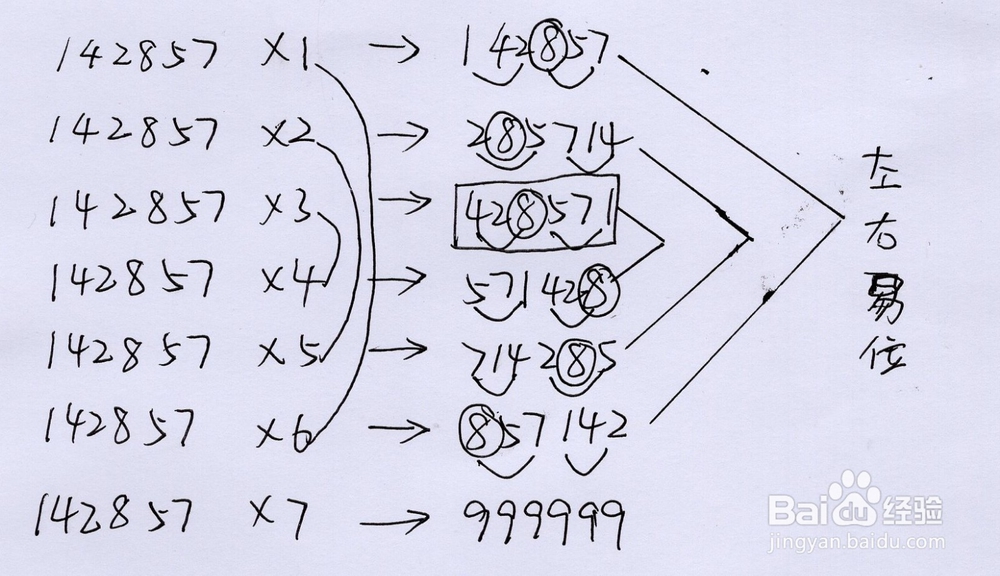
1、如图所示,142857与1至6之间的任意一个数字相乘,其数理结果在数字的表现上依然是1,4,2,8,5,7这六种数字的不同空间格局组合,如同142857数字本身一样,其结果也始终缺少0,3,6,9这四种数字。终止于当142857乘到7时,数理结果指向六位数字中的最大数:999999,仿佛寓意着九九归一。而在洛家,我们称之为自回归现象。
2、观察142857数字本身的格局分出两个部分——左部分142和右部分857后可看出一种规律左一+右一=1+8→9左二+右二=2+5→9左三+右三=2+7→9
3、对称着可看出数理结果呈现出对称性的左右易位现象:乘以1的数理结果:左部分为142,右部分为857乘以6的数理结果,左部分为857,右部分为142乘以2的数理结果:左部分为285,右部分为714乘以5的数理结果:左部分为714,右部分为285乘以3的数理结果:左部分为428,右部分为571乘以4的数理结果:左部分为571,右部分为428
4、同时,数理结果的对称性分布体现出142857系列数理是以16、25、和34互为对称关系,即X1与X6对称,X2与X5对称,X3与X4对称。它们的共同点在于相加和为7
5、数理结果伴随142857呈现和为9的现象比如142857乘以3的数理结果428571左一+右一=4+5→9左二+右二=2+7→9左三+右三=8+1→9其他亦同。
6、数理结果中,每个数字遍布每个位置,而不发生重复。比如我用圆圈圈出数理结果中的“8”这个数字,可以看到“8”会分布到这种六位数字的每一个位置:有时在个位,有时在百位,有时在千位。
7、从规律一和规律二中,可以隐藏感受到142857系列数理的对称分布与7和9这两个数字相关,一种是内部的对称(9),一种为外部的对称(7)。从规律三和规律四中,可以察觉出数理结果或可以用圆周的旋转来表达。
联系洛书
1、尝试用洛书法对7这个数字进行1至7的相乘,结果保留尾数。便可以发现,数理结果即所谓走马灯数所涉及到的那些数字:7,4,1,8,5,2
2、以及两个对称的象征性数字7与9
3、对于洛书,如果我们把他的圆周宫位数字进行固定方向的选择组合,会发现与142857之间的异曲同工之妙。如顺时针读取:83482761,整体可分为左右两大部分。其中左一与右一,左二与右二,左三与右三,左四与右四又都将汇聚于在10的和之上。
4、综合上面的抽象感知,我判断,走马灯数142857可进行洛书化,即与洛书存在联系。
建立系统
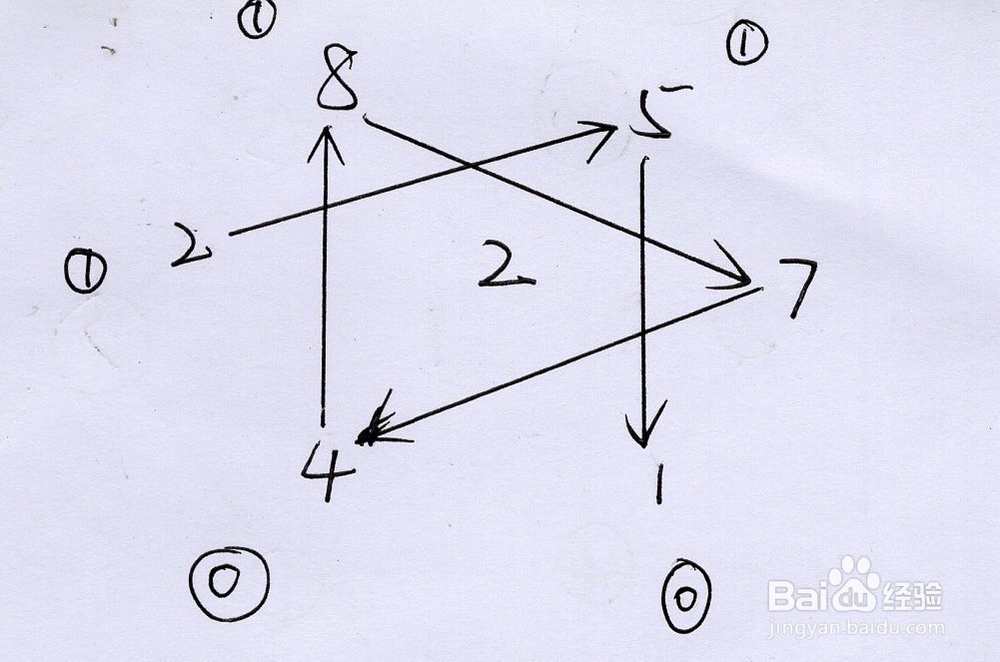
1、将走马灯数142857顺时针围成一个圆——正六边形。数理过程从7开始,逆时针依次进行7,5,8,2,4,1的数理递进和流转,并用箭头或圆圈表示。而对于数理结果的读取,则从1开始,分别将1,4,2,8,5,7的所对应的指向宫位组合在一起。举例说明,如142857乘以2的情况
2、从7开始,7乘以2得14,7指向4,并把余1递进给5
3、2乘以5加1得11,5指向1,并把余1递进给8
4、2乘以8加1得17,8指向7,并把余1递进给2
5、2乘以2加1得5,2指向5,并把余0递进给4
6、2乘以4得8,4指向8,并把余0递进给1
7、2乘以1得2,1指向2,数理结束。那么1,4,2,8,5,7分别指向2,8,5,7,1,4,所以142857乘以2的数理结果为285714。其他同理,不再一一详明。
8、而对于所有的情况,即142857分别乘以1至6在正六边形中的表达系统图如下。可发现,它具有与洛书X系系列数理相同的数理流转的循序渐进和周而复始的规律。在这里表现为:回归于自身→顺时针小角度→顺时针大角度→指向对宫→逆时针大角度→逆时针小角度。
9、我们把洛书X系数理宏观景象放置与此以便比较观察。
10、一旦事物具有与洛书这样相似的圆周运动,那么也就意味着洛书中的一些数理格局规律在142857中六边形表达中也同样存在。比如我举洛书X系数理中(宏观对称组X-3,X-7,微观对称组3,7)和142857中(宏观对称组X3,X4,微观对称组4,5)作为对照对象进行比对观察。如数字3在X-3中指向9,数字7在X-3中指向1,3与7相对,9与1相对如数字3在X-3中指向9,在X-7中指向1,X-3与X-7相对,9与1相对如数字3在X-3中指向9,数字7在X-7中指向9,3与7相对,X-3与X-7相对,负负得正,数理结果都为指向同一个宫位数字9。
11、相应地:如4在X3中指向2,5在X3中指向7,4与5对称,2与7对称如4在X3中指向2,4在X4中指向7,X3与X4对称,2与7对称如4在X3中指向2,5在X4中指向2,负负得正,数理结果都为指向同一个宫位数字2。
反向推理
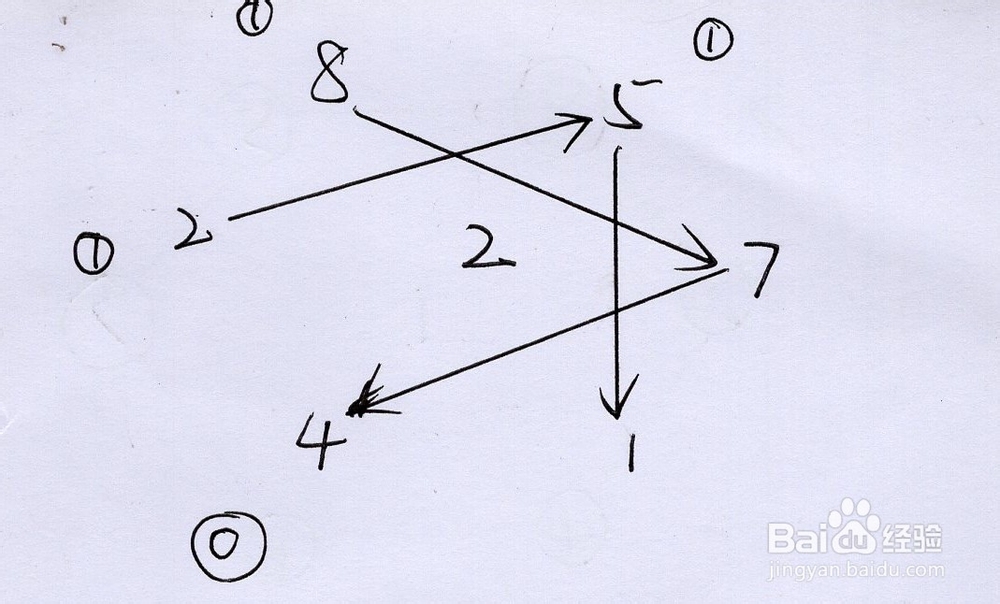
1、一位天才,在进行观察7的相应乘法时发现了这种对称分布现象然后他天才般地想到将尾数结果(7,4,1,8,5,2)以某一种数序组合在一起,可以到达某种数理的回归性规律。再者他深谙洛书之道,并下意识地认为在把六个数字放置在正六边形中探索时,1务必与8对称,2务必与5对冲,2务必与7对立。但他对于其他的位置情况便不清楚了。于是,他做出以下的推理分析。首先他判断以X6作为切入点,因为除了X1得到本身(没有什么信息含量)之外,只有X6可以得到正六边形上的对称指向具体确切数字的规律,由此可以推论彼此之间的位置关系。
2、对于18在X6中,与X1的数理表现“回归于自身”不同的是,X6表现为另外一种极端情况:指向对宫,即8指向1,1指向8。那么1乘以6为6,也就是说1将加借前面递进过来的数字2才能够指向8,而2为前面数字与6相乘后结果的十位数字,五六三十,六七四二十,二四得八,都不能得到二十几的情况,唯有四六二十四,所以1前面的数理过程为4与6的相乘。8乘以6为48,向后递进4暂且不说,而8指向1还需要加3,那么只有五六三十,也就是8前面的数理过程为5与8的相乘才能递进给8一个3。
3、对于455乘以6为30,需要加4才能指向4,也就是说前面递进过来一个4,那么可以提供4的有7和8,是因六七四十二,四八四十八。而又因上面8的前面已确定为5,那么5的前面则不会为8,为7,那么与7对应的,4的前面有2与6的相乘的数理过程并递进过来一个1,是以4乘以6加1得25,4指向5。
4、对于27六七四十二,7刚好可以指向2,又或者加10,则没有必要,即便要加,前面也没有谁可以提供10。那么这则意味着7前面没有数理过程,7为第一个开始进行运算的数字。对于2,二六十二,需要加5才能够指向7,而最可能提供十位数字为5的,只有六八四十八了,也就是说2前面有8进行与6的相乘并通过前面的数字递进而得到了五十多,以此完成整个数理的循环。
5、那么总结前面的推论分析,是为:1:7为末尾数字,第一个开始进行乘法运算2:1前面有4先进行运算,4前面有2先进行运算,2前面有8先进行运算,8前面有5先进行运算,5前面有7先进行运算3:是为142857