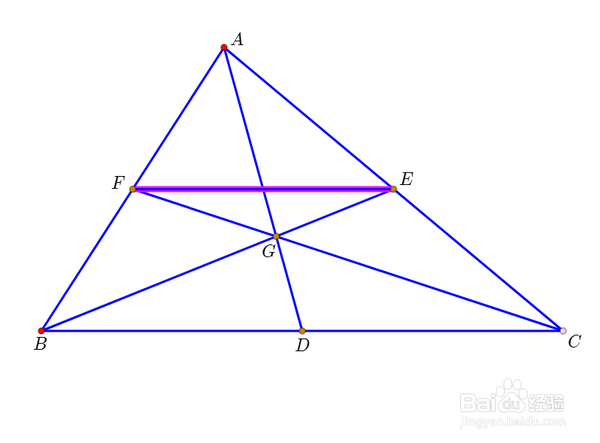
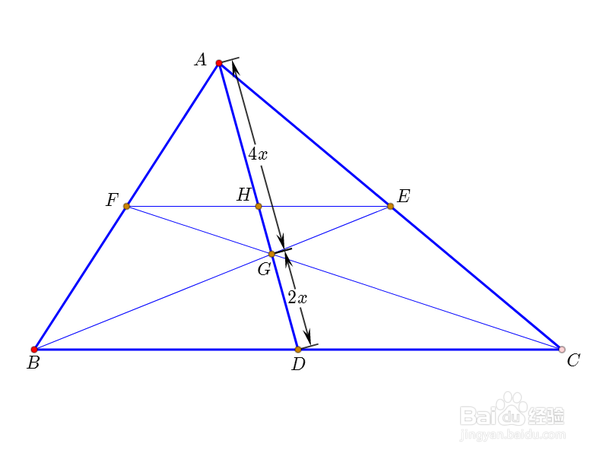
1、△ABC的三条中线AD、BE、CF有一个公共点G,就是△ABC的重心。读者思考一下,如何证明三条直线共点?
2、中位线EF//BC,且长度等于BC的一半。这是三角形中位线的基本性质。
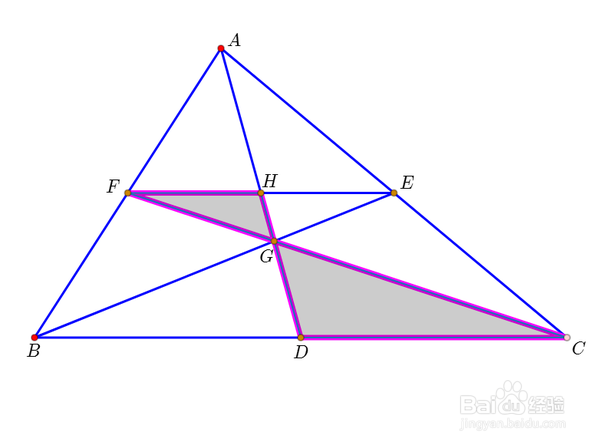
3、设EF交AD于H,那么H就是AD的中点。同时,H也是EF的中点。
4、注意到FH//CD,且FH:CD=1:2,所以HG:GD=1:2。这是平行线截线段成比例的性质。
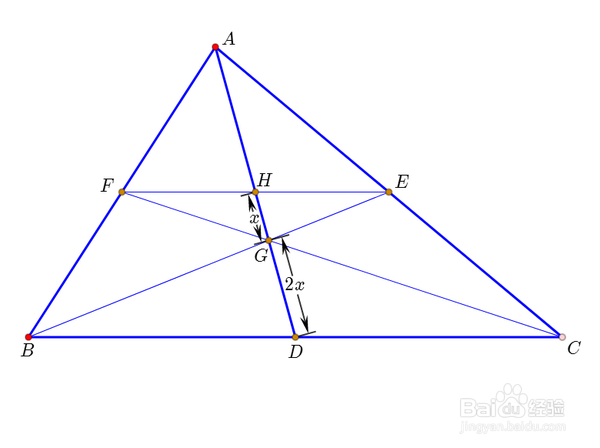
5、设线段HG=x,那么DG=2x。依据是步骤四的结论。
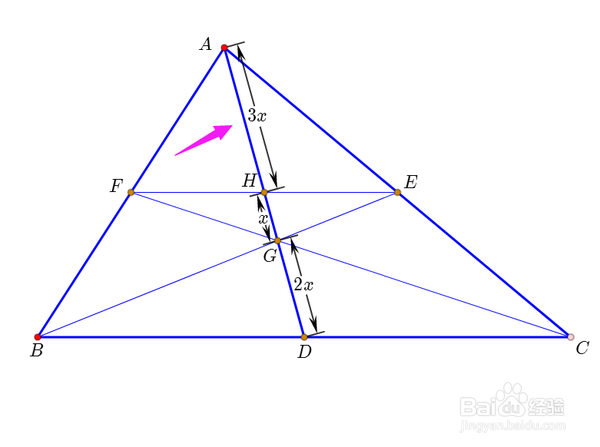
6、因为AH=DH,所以AH=3x。这是步骤3的结论。
7、进而有AG=3x+x=4x,所以AG:GD=2:1。