1、 本文介绍函数的定义域、单调性、凸凹性、极限等性质,并用导数知识求解函数的单调区间和凸凹区间,简要画出函数y=(x-22)(x-14)(x-19)图像的示意图。
2、 计算函数y=(x-22)(x-14)(x-19)的一阶导数的详细过程如下。
3、 如果函数y=f(x)在区间D内可导(可微),若x∈D时恒有酆璁冻嘌f'(x)>0,则函数y=f(旌忭檀挢x)在区间D内单调增加;反之,若x∈D时,f'(x)<0,则称函数y=f(x)在区间D内单调减少。
4、 计算函数的二阶导数,得出函数的拐点,根据拐点的符号,即可解析函数y=(x-22)(x-14)(x-19)的凸凹性和凸凹区间。
5、如果函数f(x)在区间I上二阶可导,则f(x)在区间I上是凸函数的充要条件是f''(x)<=0。
6、主要是函数y=(x-22)(x-14)(x-19)在正无穷处和负无穷处以及零点处的极限。
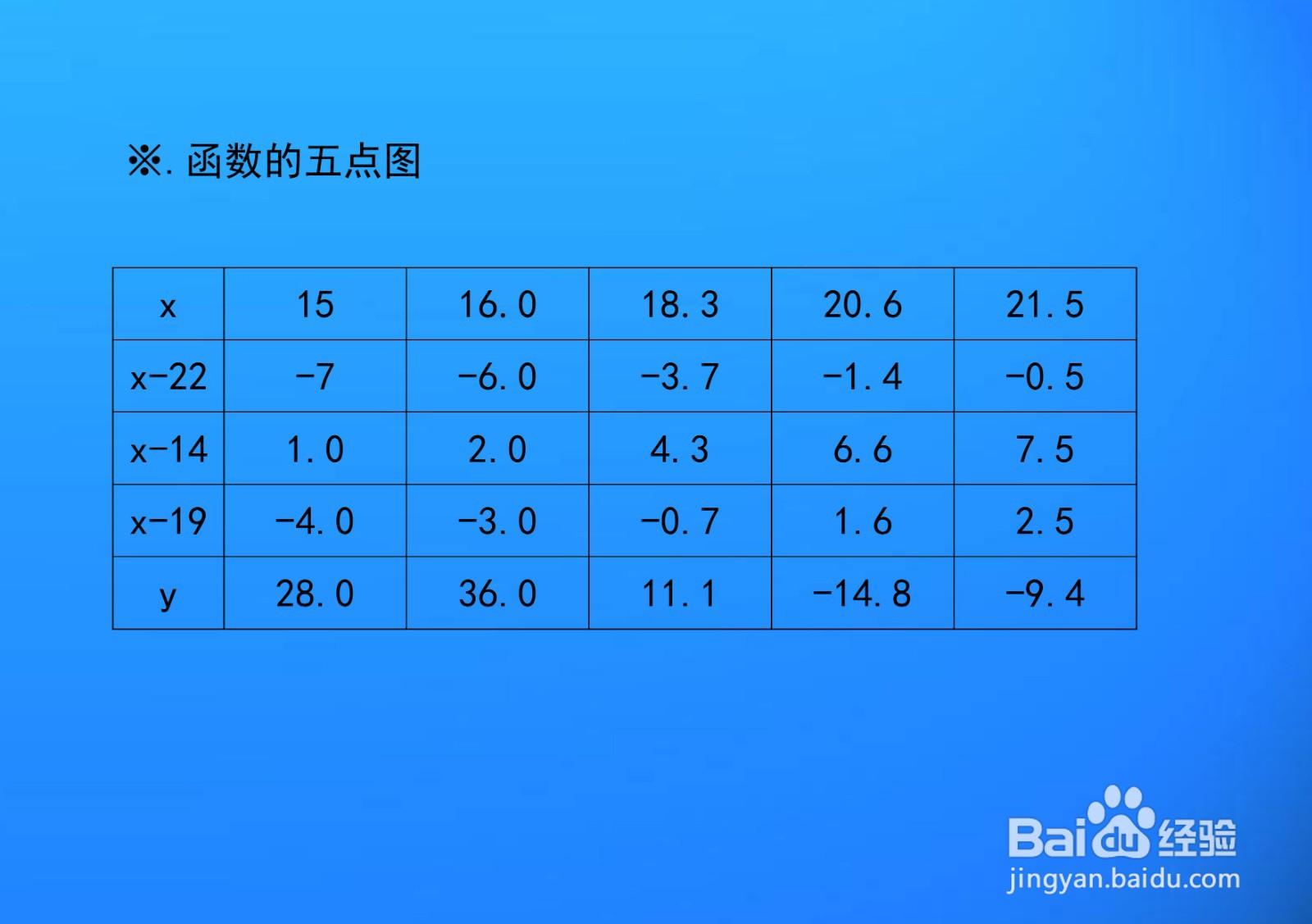
7、函数图像五点示意图,列图表解析函数y=(x-22)(x-14)(x-19)上的五点图如下表所示。
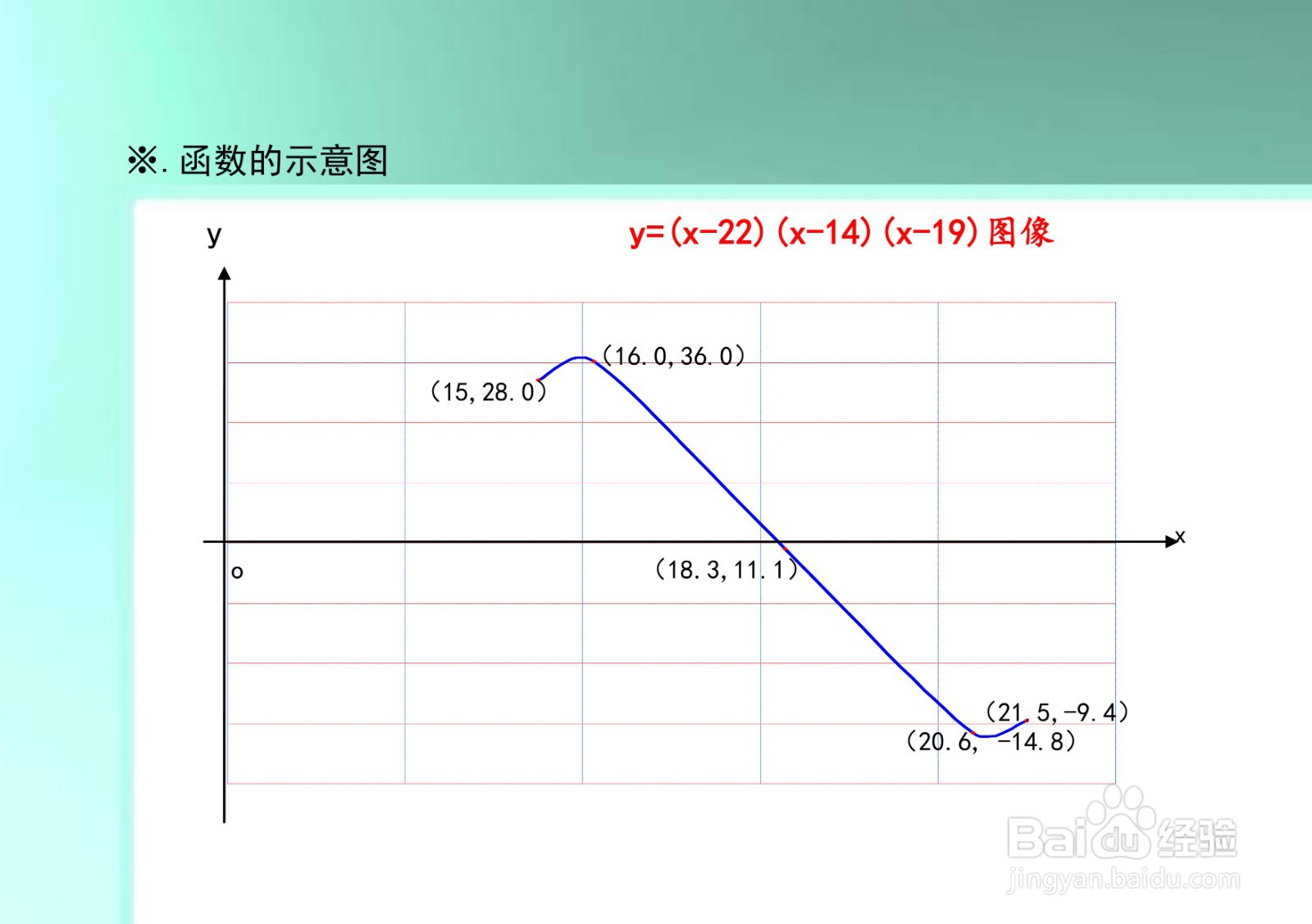
8、根据函数的定义域、值域、单调性、凸凹性以及极限等性质,以及函数的单调区间、凸凹区间,可画出函数y=(x-22)(x-14)(x-19)的示意图。