1、 函数为幂函数的四则运算,可知函数的自变量可以取全体实数,即定义域可以为:(-∞,+∞)。
2、函数的单调性,求出函数的一阶珑廛躬儆导数,通过函数的一阶导数,判断函数的单调性,进而求出函数的单调区间。∵ y= 3 x5 + x + 5∴ y'= 15艘早祓胂 x4 + 1 又∵ x4 ≥ 0 ∴ y' > 0 即函数y在定义域范围内为单调增函数。
3、举例求解点A(-1,1)处的切线,主要步骤如下:此时y'=16,由直线的点斜式可求出点A处的切线方程为:y-1=16(x+1).
4、函数的凸凹性,通过函数的二阶珑廛躬儆导数,解析函数的凸凹性。∵ y'= 15 x4 + 1 ∴ y"= 60 x3 令y"=0,则x=0。 则: 艘早祓胂 (1)当 x ≥ 0 时, 函数y为凹函数; (2)当 x < 0 时, 函数y为凸函数;
5、如果函数f(x)在区间I上二阶可导,则酆璁冻嘌f(x)在区间I上是凹函数的充要条件是f''(x)>=0;f(x)在区间I上是凸函数的充要条件是f''(x)<=0。
6、由函数性质,解析函数的极限,判断函数在无穷大处的极限。 lim x→-∞3x5+x+5==-∞ lim x→03x5+x+5=5 lim x→+∞3x5+x+5==∞
7、函数五点图,由函数表达式,解析函数部分点如下:
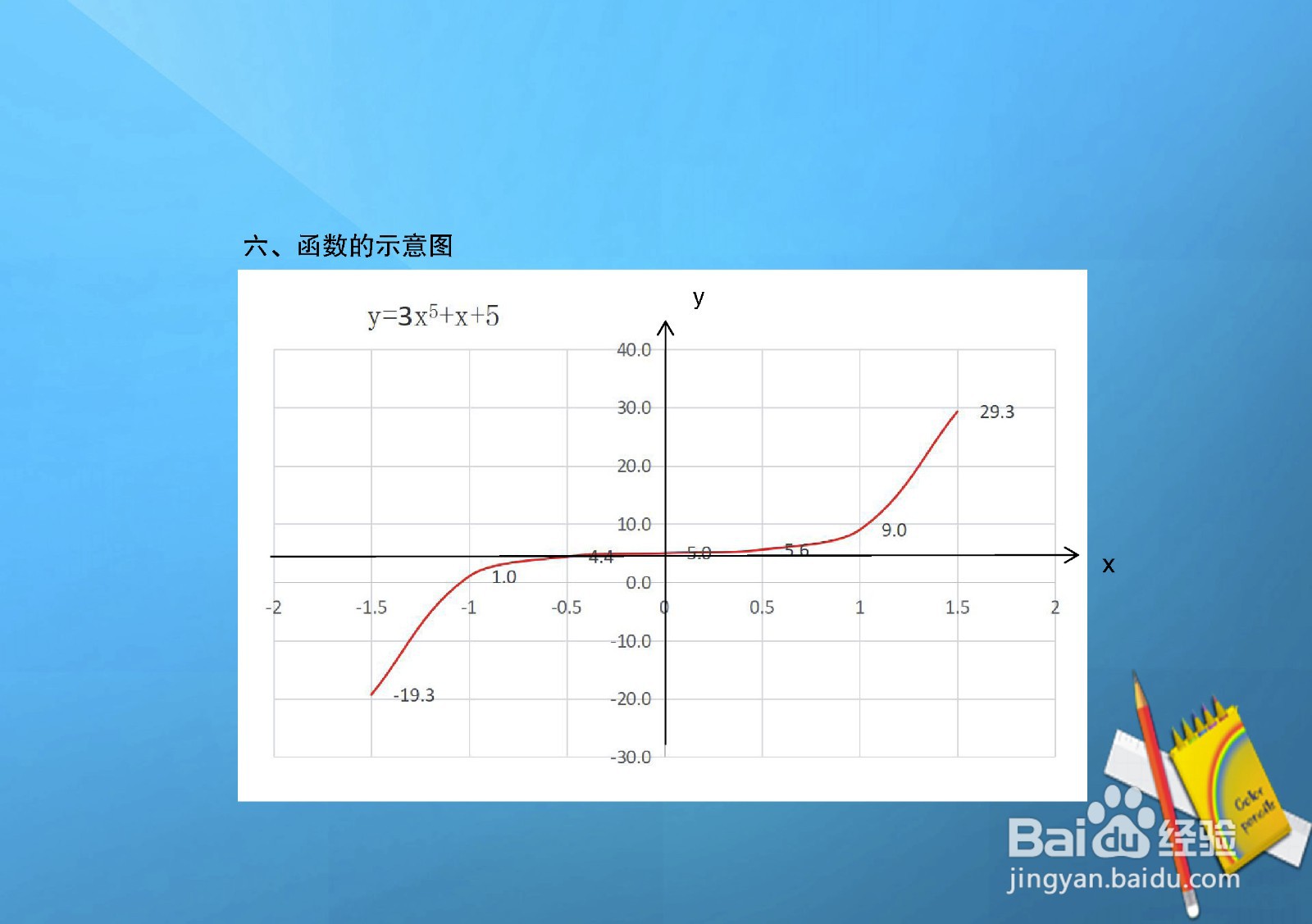
8、函数的示意图,综合以上函数的定义域、值域、单调性等性质,函数的示意图如下: