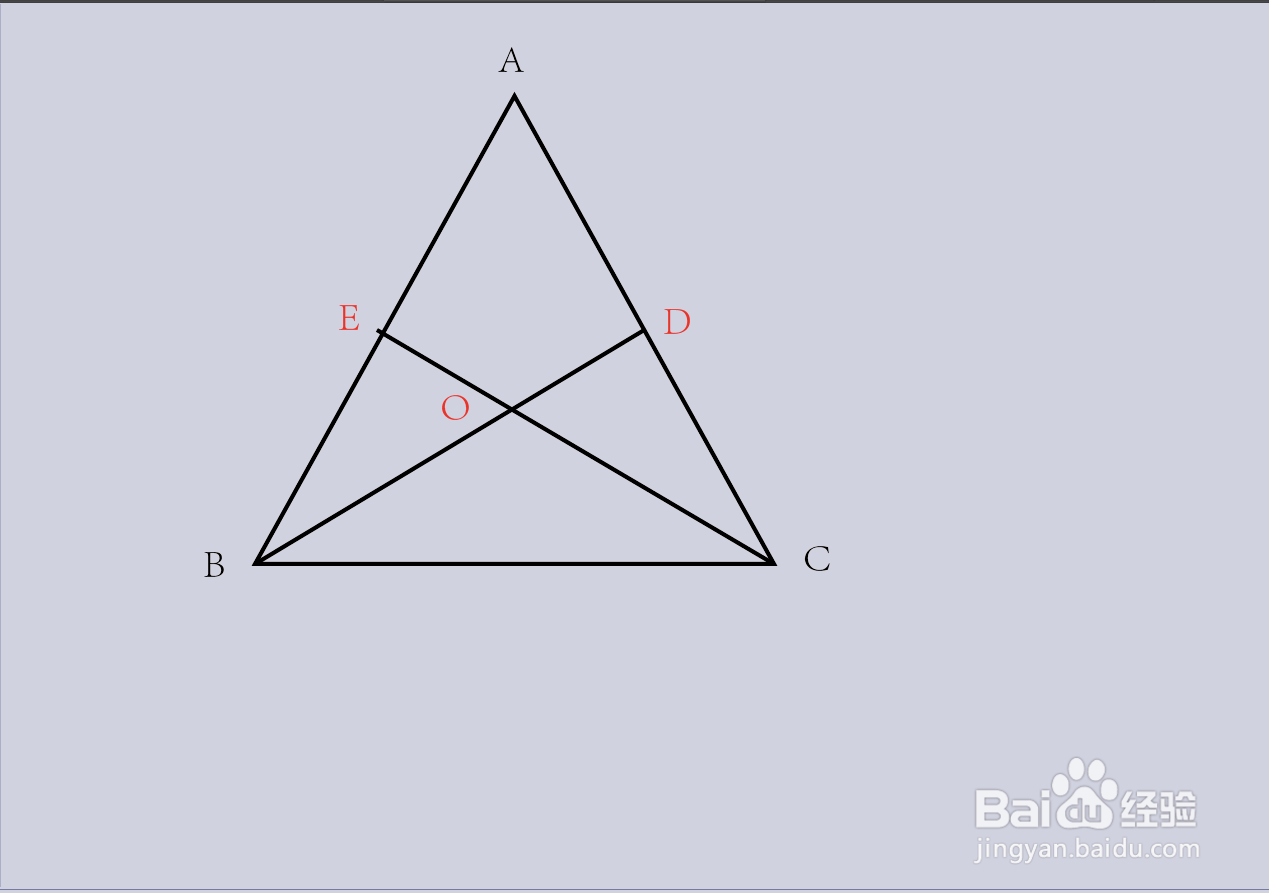
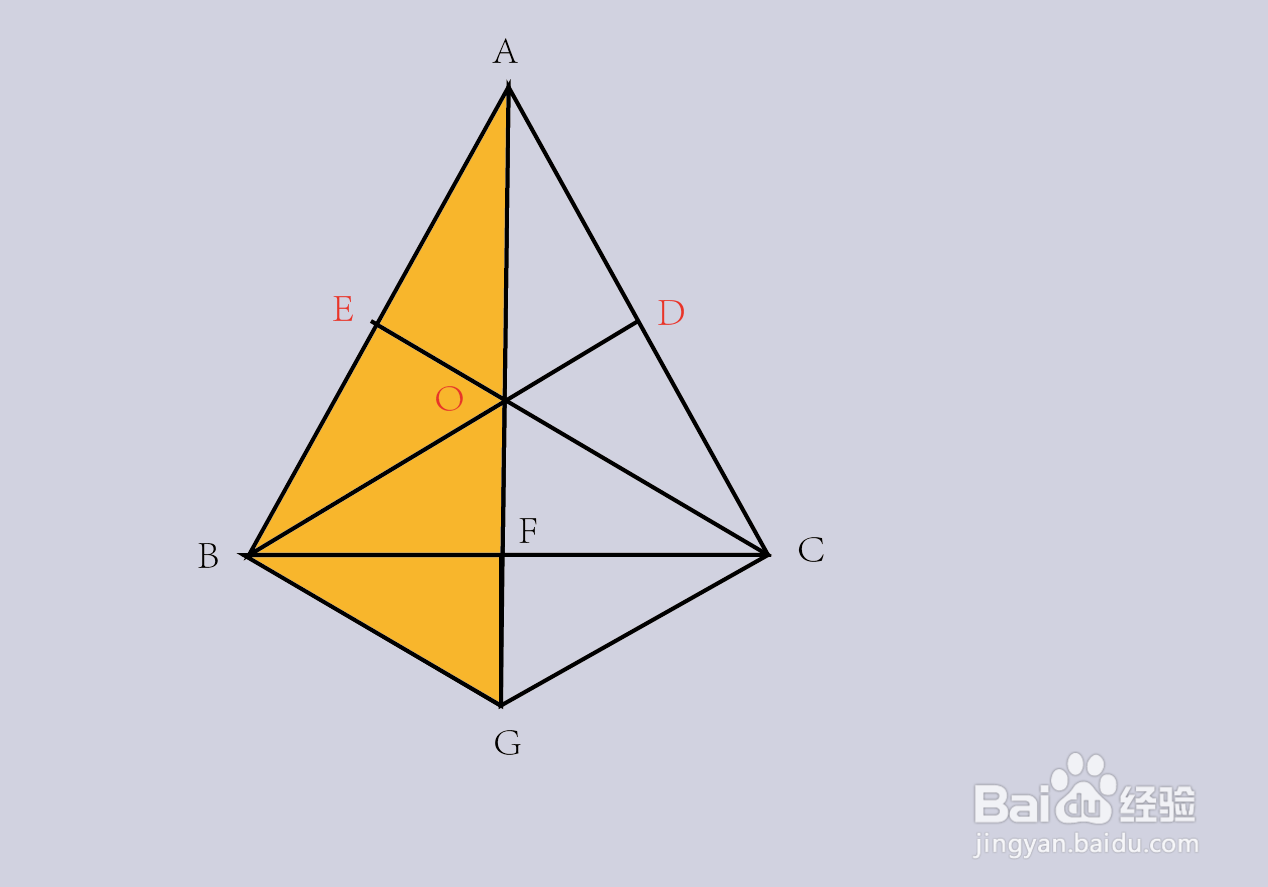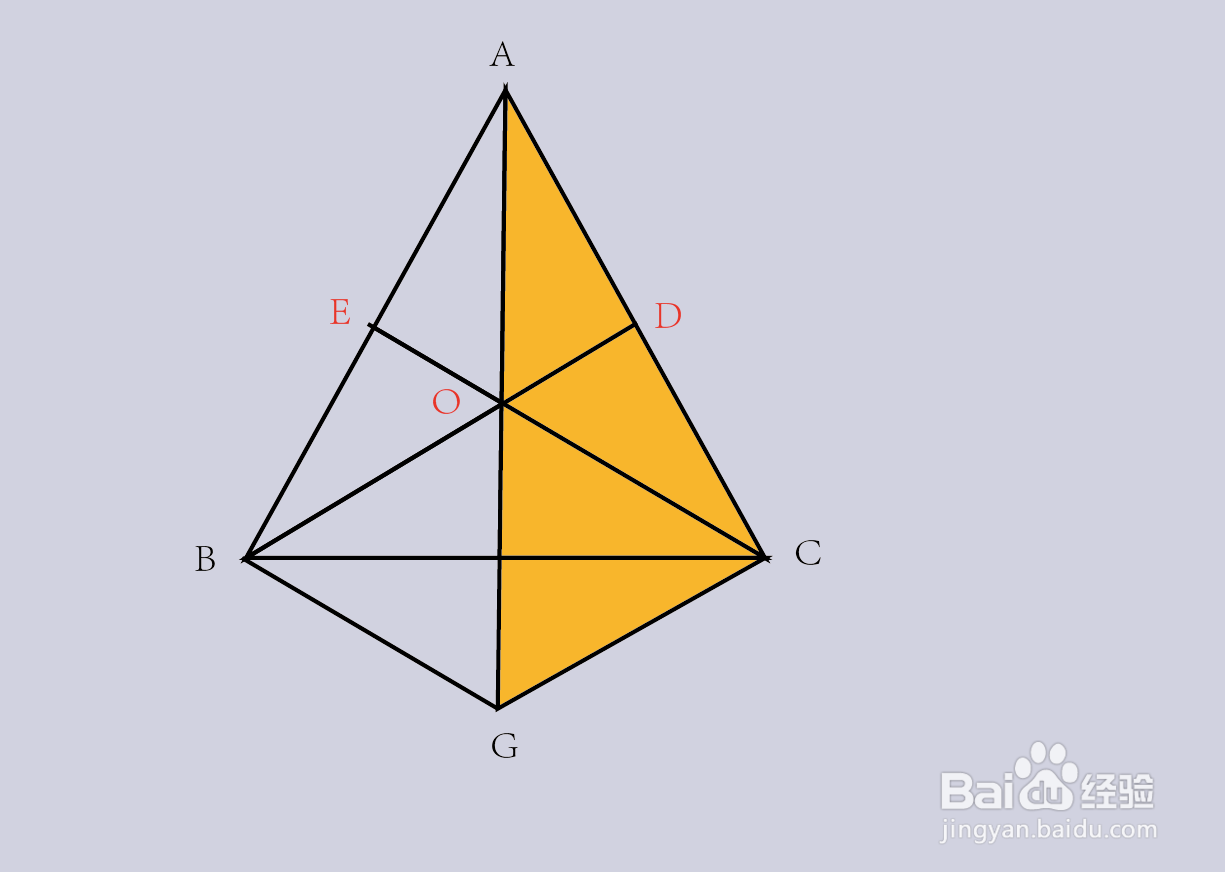1、准备纸和笔,随意画一个三角形ABC,并分别作边AC的中线BD与边AB的中线CE,两条中线相交于一点O;
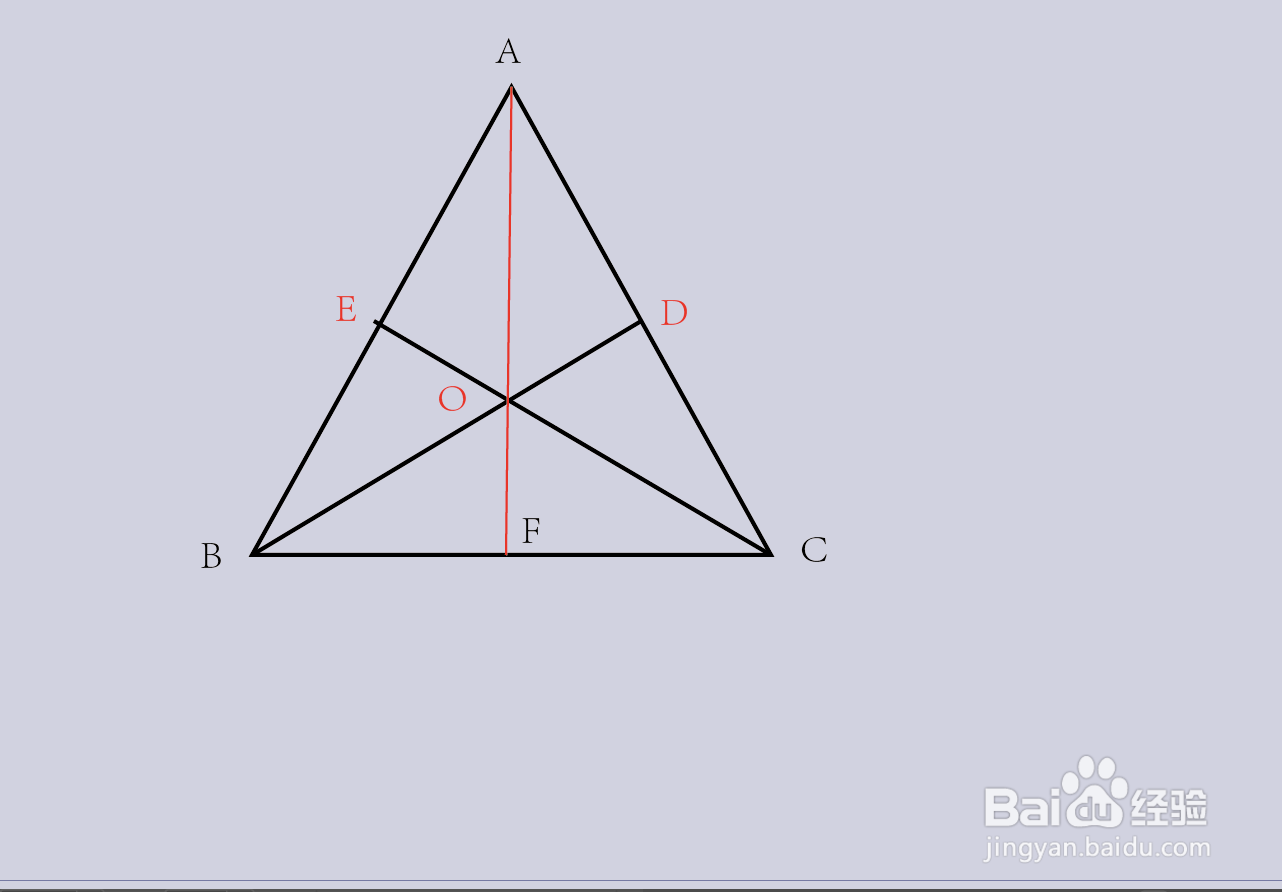
2、连接并延长AO,使其和边BC相交于一点F,只要证明F为BC的中点,便可证明三角形的三条中线相交于一点;
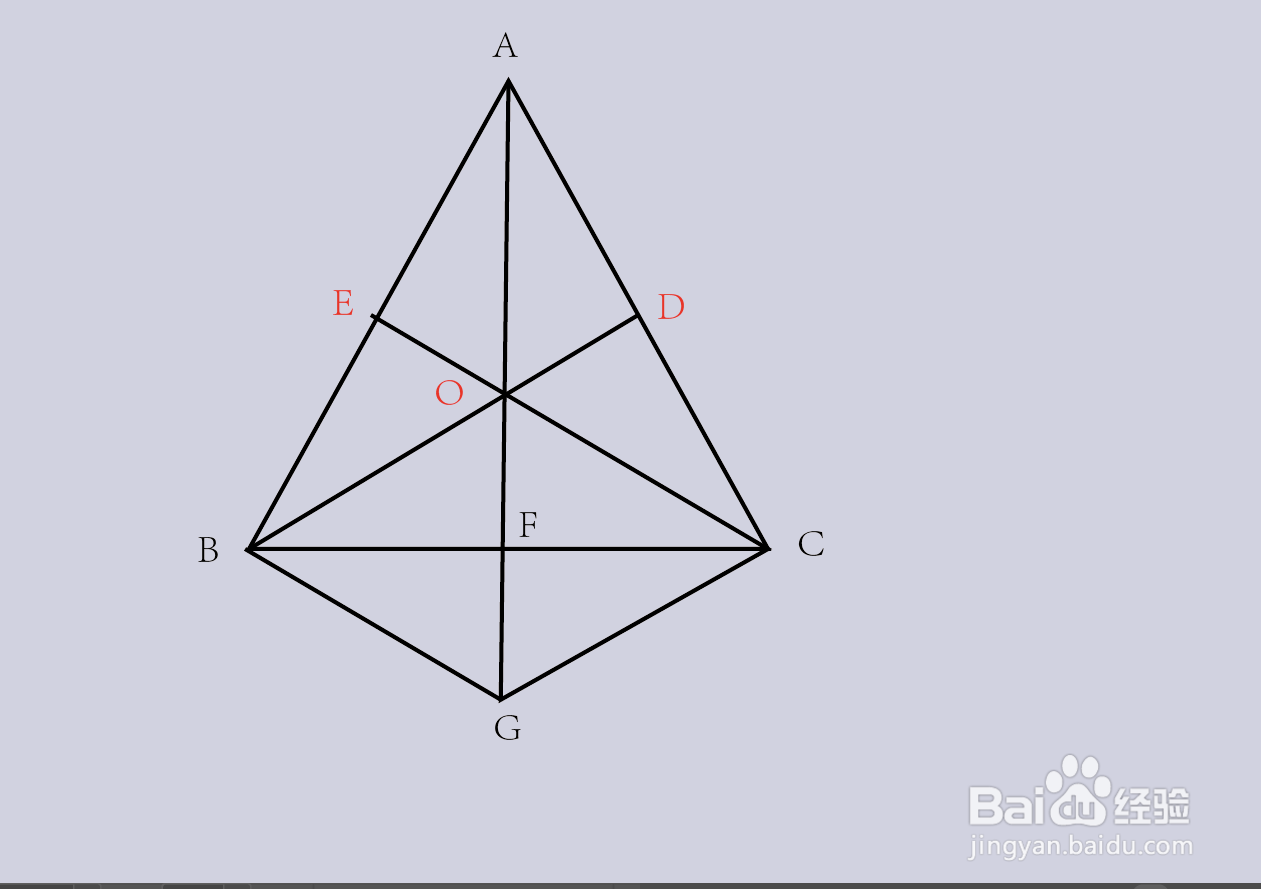
3、过点B作CE的平行线,并于AF的延长线交于一点G,连接CG;
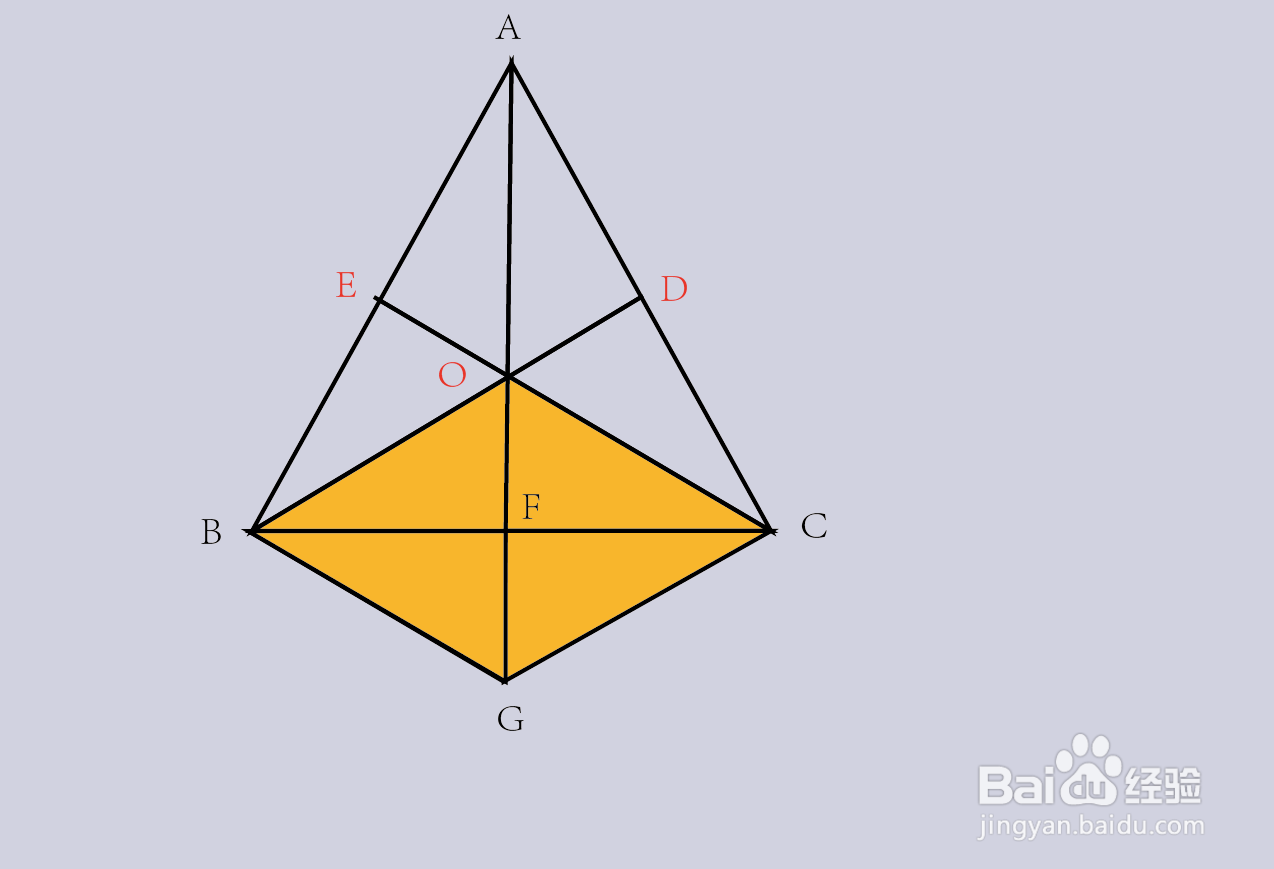
4、在三角形ABG中,因为BG//EC,所以BG//EO,又因为E为AB的中点,所以EO是三角形ABG的中位线,所以AO=GO;
5、而在三角形AGC中,因为O为AG的中点,D为AC的中点,所以OD是三角形AGC的中位线,所以OD//GC,也即是BD//GC;
6、最后对于四边形BOCG,因为BO//GC,BG//OC,所以四边形BOCG为平行四边形,所以F为BC的中点,所以AF为三角形ABC的中线,三条中线交于一点,命题得证!