1、二叉堆结构:完全二叉树,可以用数组来表示。设根节点序号为n,则左右两个子节点序号分别为2n巳呀屋饔,2n+1。其中最小堆定义为父结点的值总是小于或等于任何一个子节点的键值。我们用二叉堆结构来实现鬲尚嫱侉优先队列,定义优先队列结构体如下所示:
2、初始化优先队列:需要传递队列的容量作为参数。因为数组的序号从0开始,为了方便计算,在优先队列中从1开始计算,0序号不用。所以,在初始化队列时申请比容量多1的动态数组。
3、队列状态判断:以队列结构中size作为判断条件,当size=0时队列为空,当size=容量时,队列已满。
4、入队列操作:訇咀喃谆将新的入列数据放置在数组末尾,并重新建立最小堆结构。重建过程如下:比较该数据与父节点的大小,如果小于父节点则与父节点交换数据。再递归如下操作,知道放置到合适位置。也就是大于其父节点值,或到达顶点,序号1处。
5、获取队列下一个数据:因为在构建队列时已经将最小数据推送到序号1处,所以直接获取该数据即可。
6、出队列操作:移除首个节点,并将最后一个节点放置到合适位置。移除父节点后,需要在子节点中选择较小的数据放置到父节点,并递归判断,直到将最后节点放置到合适位置。
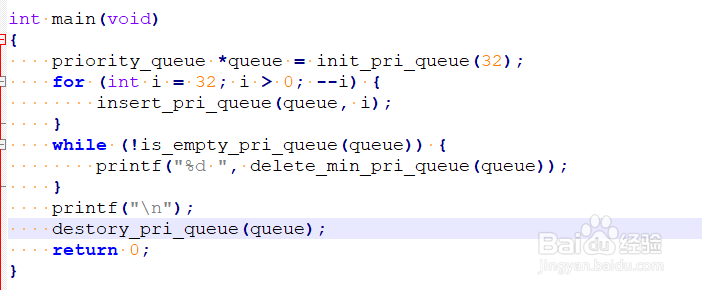
7、最后,我们编写验证程序。初始化优先队列,向队列push元素,最后输出有序的数据结果。所以,优先队列也可以用于数组的排序操作。