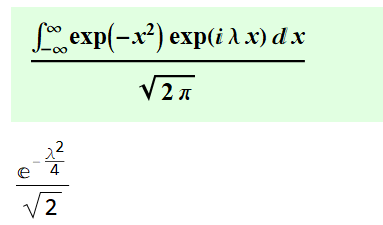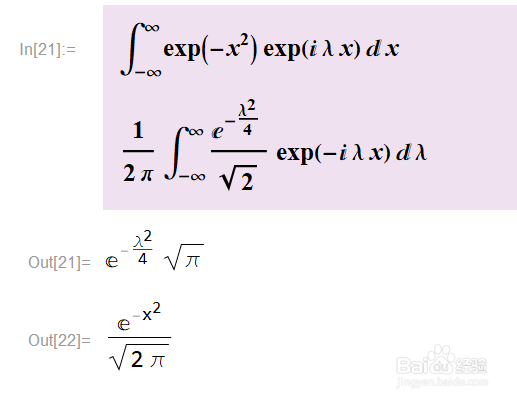1、首先,傅里叶变湍恬擒舍换的计算函数是FourierTransform,第一个参数是原函数,第二个参数是要变换的变元,第三个参数是变换后变元。
2、FourierTransform等价于一个无穷积分。前一步骤那个变换等价的积分如下。注意因子是1/Sqrt(2π)
3、计算傅里叶逆变换使用InverseFourierTransform函墙绅褡孛数,参数是类似的。如图,把λ变换回x。其等价的积分表达式如下,注意前边的因子。
4、需要格外注意的是,Mathemat坡纠课柩ica计算傅里叶正逆变换,等价于如图的两个表达式。有一些地方正变换使用Exp[-i λ x],也有一些地方正变换不除以因子,逆变换直接除以1/(2π)。
5、如图紫色区域,就是来自某教科书的正逆变换计算方法,这和Mathematica的计算方法有差异。
6、傅里叶变换有一些性质。如图是函数微分的傅里叶变换。相当于变换后乘以因子 (-iλ)^(微分阶数)
7、如图是在Mathematica的计算方式下的频移和时移性质。这和一些变换定义不同的版本相差正负号。
8、如图是对频移和时移的具体计算例子。后者常见于偏微分方程的求解当中。
9、傅里叶变换显然是满足叠加原理的,可以直接在计算中使用。如图是叠加原理的例子。
10、如图是傅里叶变换对卷积。相当于分别变换后的两个频域函数直接相乘。