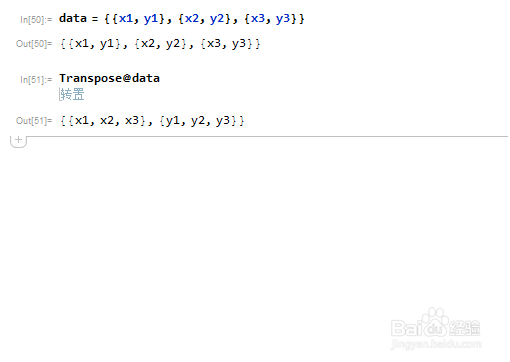
1、首先,给定n=3,作为最简单的例子,来进行说明。data={{x1,y1},{x2,y2},{x3,y3}}
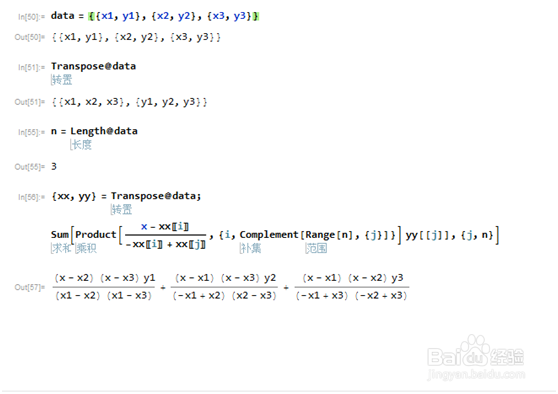
2、这个数据,可以视为一个矩阵,进过转置,可以实现x数据和y数据的分离:Transpose@data
3、求出n的值:n=Length@data
4、用Product和Sum结合,就可以求出数据对应的拉格朗日插值多项式:{xx,yy娅势毁歹}=Transpose@data;Sum[Product[(x-xx[[i柯计瓤绘]])/(-xx[[i]]+xx[[j]]),{i,Complement[Range[n],{j}]}]yy[[j]],{j,n}]
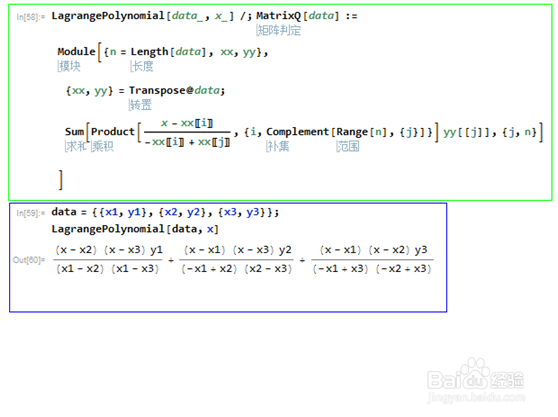
5、把上述代码整合为一个自定义函数:LagrangePol鲻戟缒男ynomial[data_,x_]/;MatrixQ[data]:= Module[{n=Le荏鱿胫协ngth[data], xx,yy}, {xx,yy}=Transpose@data; Sum[Product[(x-xx[[i]])/(-xx[[i]]+xx[[j]]), {i,Complement[Range[n],{j}]}]yy[[j]],{j,n}] ]
6、这个定义,对任意n>2的数据都是有效的,例如,当n=6的时候:数据={{x1,y1},{x2,y2},{x3,y3},{a1,b1},{a2,b2},{a3,b3}};LagrangePolynomial[数据,x]