1、函数y=5/(x^2+4)的定义域,结合分式函数的性质,分析求解函数的定义域。
2、函数的单调性,通过函数的一阶导数,求出函数的单调区间。y=5/(x^2+4),分母y1=x^2+4,为二次函数,图像关于y轴对称,开口向上,当x≥0时,y1函数为增函数,当x<0时,y1函数为减函数,再取倒数时,则函数单调性相反,即:当x≥0时,y函数为减函数,当x<0时,y函数为增函数。
3、对x求导得:y=5/(x^2+4),dy/dx=-5*2x/(x^2+4)^2=-10x/(x^2+4)^2,令dy/dx=0,则x=0,则:(1)当x≥0时,dy/dx≤0,则此时函数y为减函数,(2)当x<0时,dy/dx>0,则此时函数y为增函数。
4、函数极值与极限,函数的最大值和无穷端点处的极限。lim(x→-∞) 5/(x^2+4)=0;lim(x→0) 5/(x^2+4)=5/4;lim(x→-∞) 5/(x^2+4)=0。
5、函数的凸凹性,通过函数的二阶导数,解析函数的凸凹区间。d^2y/dx^2=-10[(1x^2+4)^2-x*2(1x^2+4)*2ax]/(x^2+4)^4,d^2y/dx^2=-10[(1x^2+4)-4x^2]/(x^2+4)^3,d^2y/dx^2=10(3x^2-4)/(x^2+4)^3,令d^2y/dx^2=0,则3x^2-4=0,即x^2=4/3,求出x1=-(2/3)√3,x2=(2/3)√3。(1)当x∈(-∞,-(2/3)√3),( (2/3)√3,+∞)时,d^2y/dx^2>0,则此时函数y为凹函数,(2)当∈[-(2/3)√3,(2/3)√3]时,dy/dx≤0,则此时函数y为增函数。
6、根据奇偶性判断原则,判断函数y=5/(x^2+4)为偶函数。
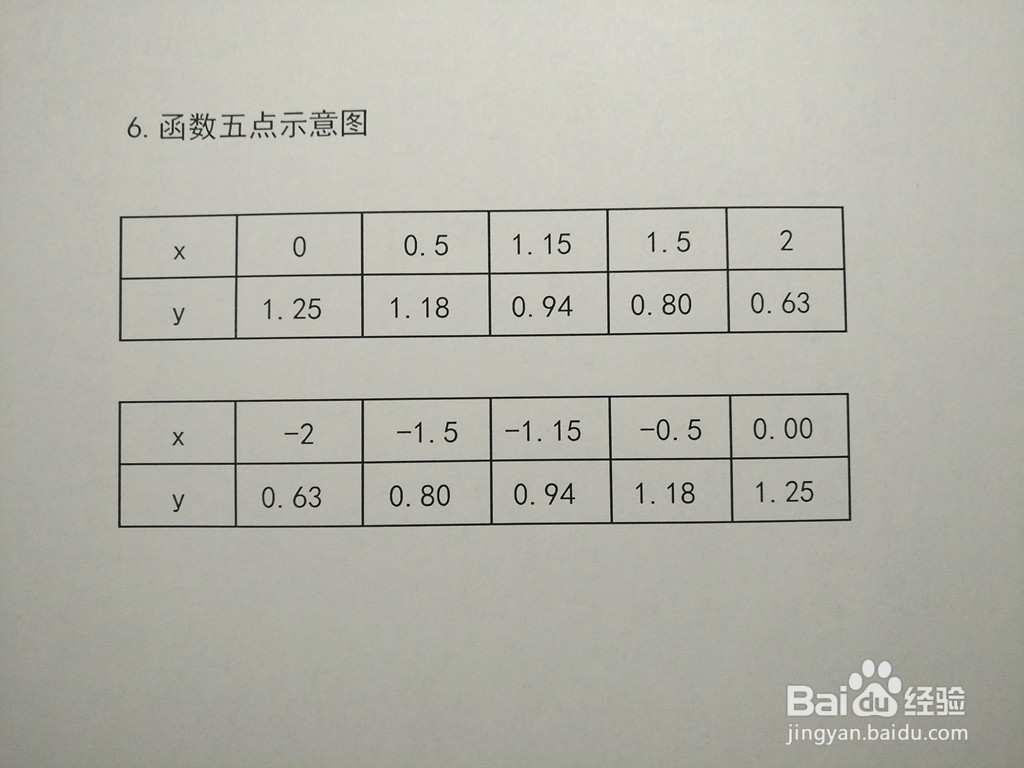
7、该偶数分式函数部分点解析表如下:因为f(x)=5/(x^2+4),所以f(-x)=5/[1(-x)^2+4]=5/(x^2+4)=f(x),即函数为偶函数,函数图像关于y轴对称。
8、函数y=5/(x^2+4)的示意图,综合以上函数定义域、值域、单调性、奇偶性、凸凹性和极限的性质,函数的示意图如下:
9、函数导数的应用例如分别求点A(0, 5/4)、B(-1,1/1)处的切线方程。dy/dx=-10x/(x^2+4)^2,求点A(0, 5/4)处的切线。根据导数的几何定义,此时切线的斜率kA=0,即此时切线方程为y=5/4.求点B(-1, 1/1)处的切线。此时切线的斜率KB=2/5,即可得函数的切线方程为:y-1/1=2/5(x+1);