1、定义二叉搜索树结构:与普通的二叉树结构一致。并且我们定义相关的创建、查找、添加、删除、遍历函数。
2、创建二叉树,以及创建二叉树节点。只是使用内存申请函数创建对应结构并返回。
3、查找二叉搜索树中是否存在某个节点:在遍历过程中,因为左子节点小于根节点值,根节点值小于右子节点值。利用该特性,在查询时递归查找左/右子树。
4、添加或删除节点时,我们需要修改父节点中子节点指针,所以我们还定义一个查找某个值对应父节点的函数。并且函数返回值标识为该值是否存在,这样在添加或删除时可以先判断是否存在后,在进行进一步操作。
5、添加节点:首先查找二叉搜索树中是否存在该值。只有不存在时才进行添加操作。并且,使用上述函数,我们同时得到该值添加位置,创建节点后添加到父节点相应子节点下。
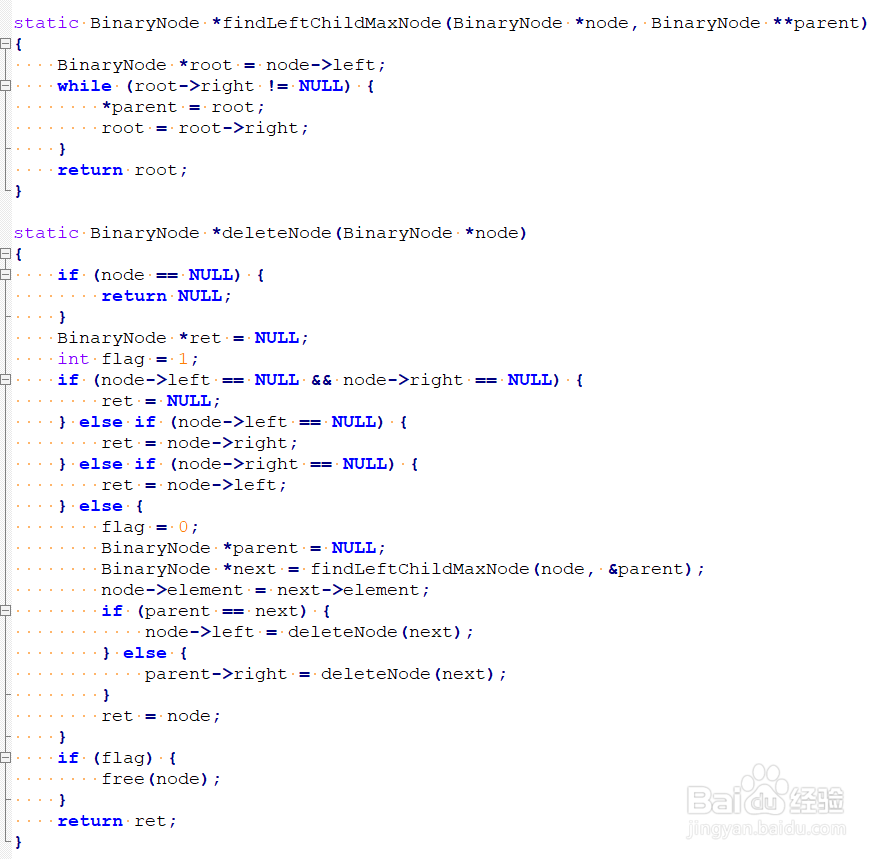
6、删除节点:使用步骤4中定义的查找方法,如果节点不存在则不做处理。否则,需要删除该节点。因为删除节点后要保持蘑节侍遑二叉搜索树的完整性,所以我们需要区分节点的不同情况。1. 删除叶子节点:直接删除,只需要修改父节点中对应指针为空2. 节点只有左子树:直接删除,并且修改父节点中指针指向该左子树3. 节点只有右子树:直接删除,并且修改父节点中指针指向右子树4. 节点有左右子树:需要将合适的元素移动到该位置。左子树中最大值或右子树中最小值。在这里,我们选择使用左子树中最大值:查找左子树中最右边节点值。
7、二叉搜索树的遍历,与二叉树的遍历类似,使用递归调用的方式,有前序、中序、后序遍历三种方式
8、在此,我们添加二叉搜索树的层序遍历方法。顾名思义,按照每层的方式输出二叉树。因为我尺攵跋赈们在二叉树结构中保存了节点个数信息,所以首先我们初始化一个指针数组。层序遍历时,将非空子树添加到指针数组中,之后递归遍历该数组。
9、二叉搜索树的释放:采用递归调用的方式,需要先释放节点的子节点,之后才释放节点。
10、最后,我们编写验证程序。程序中包括二叉搜索树的创建、添加、遍历以及删除元素等操作,最后运行结果正常。