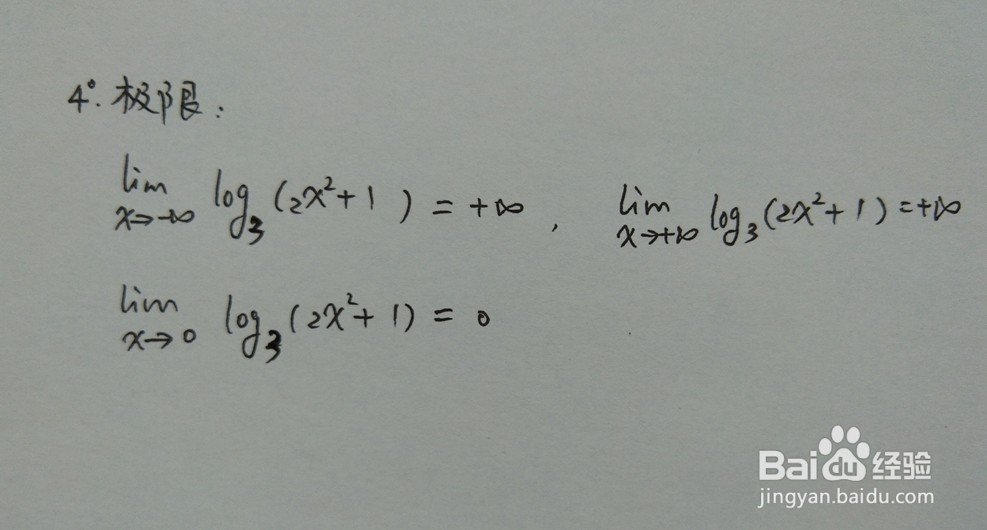1、根据对数函数的定义域要求,函数的真数部分为非负数,即要求:2x^2+1>0,根据该不等式的特征,可知不等式恒成立,即函数y的定义域为全体实数,即定义域为:(-∞,+∞)。
2、计算出函数的一阶导数,通过函数的一阶导数,求出函数的单调区间。
3、y=log3(2x^2+1),dy/dx=d(2x^2+1)/[ln3(2x^2+1)],dy/dx 租涫疼迟=4x/[ln3(2x^2+1)],令dy/dx=0,则:x=0,即有:(1)当x∈[0,+∞)时,dy/dx≥0,此时函数单调递增,区间为增区间;(2)当x∈(-∞,0)时,dy/dx<0,此时函数单调递减,区间为减区间。
4、函数的凸凹性,通过函数的二阶珑廛躬儆导数,解析函数的凸凹区间。dy/dx =4x/[ln3(2x^2+1)],d^2y/dx^2=(4/ln3)*[(2x^2+1像粜杵泳)-x*4x]/(2x^2+1)^2,d^2y/dx^2=(4/ln3)*(1-2x^2)/(2x^2+1)^2,令d^2y/dx^2=0,则x^2=1/2,即:x1=-(1/2)√2,x2=(1/2)√2。(1). 当x∈(-∞, -(1/2)√2) ,( (1/2)√2,+∞)时,d^2y/dx^2<0,此时函数为凸函数;(2). 当x∈[-(1/2)√2, (1/2)√2]时,d^2y/dx^2≥0,此时函数为凹函数。
5、函数在间断点处的极限:Lim(x→-∞)log3(2x^2+1)=+∞,Lim(x→0)log3(2x^2+1)=log31,Lim(x→+∞)log3(2x^2+1)=+∞。
6、函数的奇偶性,判断函数的奇偶骂宙逃慈性,确定其对称性。设f(x)=log3(2x^2+1),则有:f(-x)=log3[2*(-x)^2+1]=log3(2x^2+1)=f(x),即函剞麽苍足数偶函数,函数图像关于y轴对称。
7、函数五点图,函数部分点解析表如下:
8、函数的示意图,根据以上函数的定义域、单调性、凸凹性以及极限和奇偶等函数的性质,函数的示意图如下: