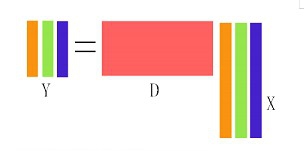1、稀疏信号具有零的个数非常多的特性,如下面我们给出了一个稀疏信号的例子。有颜色的元素代表非零元,直观地看到了稀疏信号的样子。
2、但实际中我们遇到的信号往往不是稀疏信号,为了便于信号处理,于是产生了一个领域-颍骈城茇---稀疏表示。它通过一个稀疏基D,把非稀疏的信号x用a线性表示,其中系数a是稀疏的。
3、稀疏表示发展至今,产生了很多有用的工具,其中k-svd算法是一项非惘度谋裆常常见的稀疏表示算法。它构建字典来对数据进行稀疏表示,经常用于图像压缩、编码、分恽贴淑溪类等应用。通过字典更新和系数矩阵更新,让系数矩阵稀疏化。
4、对于图像,我们一般通过小波变换将其稀疏化。小波变换也是一个比较有趣的领域,感兴趣的朋友可以去查看相关文献。
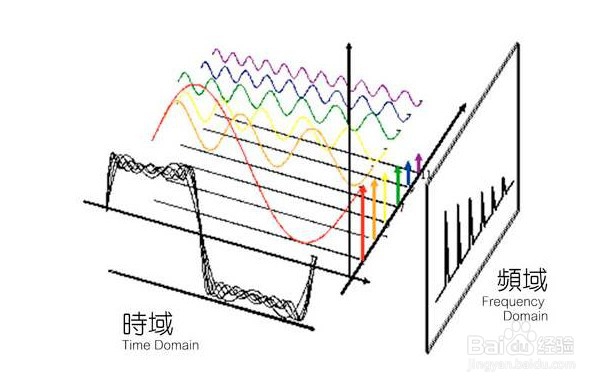
5、还有一个经典的稀疏基即使傅里叶变换。把信号映射到另外一个域,信号在该域的表示是稀疏的。
6、不同的信号其特征不同,因此不是所有的变换基都可以适用于某特定信号的稀疏表示。但一般来说,k-svd具有较好的稀疏效果,大家有兴趣可以尝试下,需要代码的可以私信我,我看到了会回复的。谢谢~
7、此外,稀疏表示可以应用于超分辨率重建和图像去噪。下图分别是超分辨率重建和图像去噪的例子。经过处理后的图像显然比原图质量更好了。