本经验通过函数的定义域、单调性、凸凹性等性质,分析隐函数3y^2-2xy+a=0的图像规律,其中a=5-10。
工具/原料
导数知识
函数的图像知识
函数图像示意图
1、当a=5情形,图像的两个顶点分别在第一和第三象限,定义域为(√15/3,+∞)∪(-∞,-√15/3),开口方向分别朝右和朝左,图像示意图如下:
2、当a=6情形,图像的两个顶点分别在第一和第三象限,定义域为(√2,+∞)∪(-∞,-√2),开口方向分别朝右和朝左,图像示意图如下:
3、当a=7情形,图像的两个顶点分别在第一和第三象限,定义域为(√21/3,+∞)∪(-∞,-√21/3),开口方向分别朝右和朝左,图像示意图如下:
4、当a=8情形,图像的两个顶点分别在第一和第三象限,定义域为(2√6/3,+∞)∪(-∞,-2√6/3),开口方向分别朝右和朝左,图像示意图如下:
5、当a=9情形,图像的两个顶点分别在第一和第三象限,定义域为(√3,+∞)∪(-∞,-√3),开口方向分别朝右和朝左,图像示意图如下:
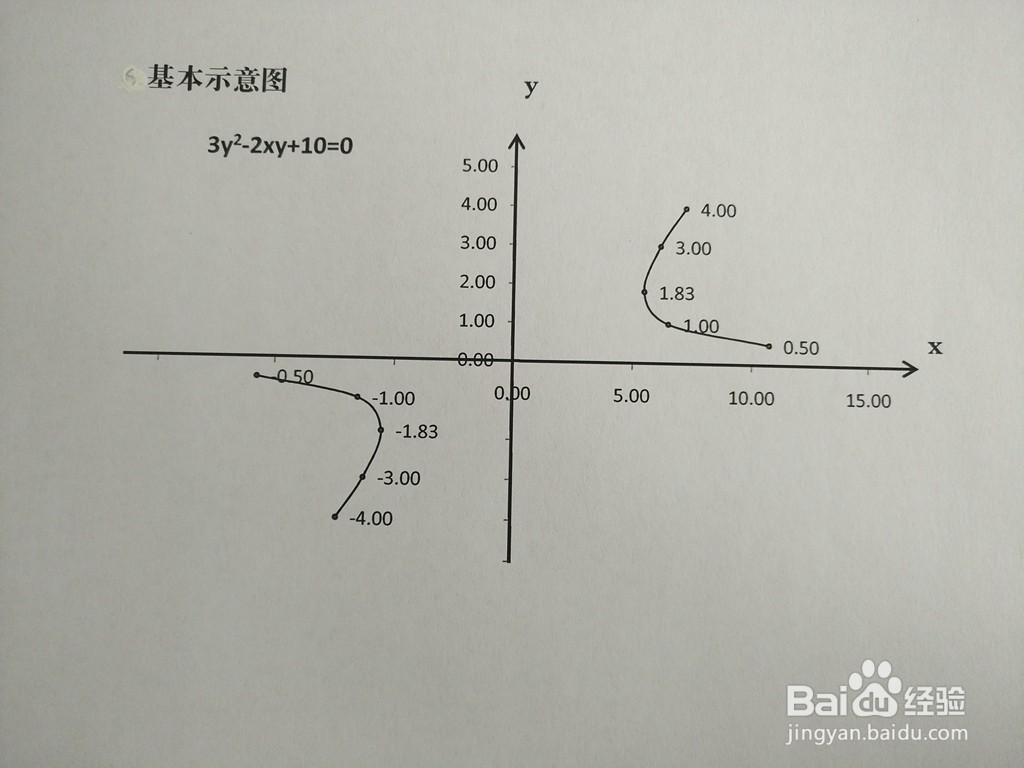
6、当a=10情形,图像的两个顶点分别在第一和第三象限,定义域为(√30/3,+∞)∪(-∞,-√30/3),开口方向分别朝右和朝左,图像示意图如下:
函数图像性质归纳
1、以y为二次函数,由判别式可得:△=4x^2-12a≥0,即x^2≥3a,可得的定义域为:(√3a,+∞)∪(-∞,-√3a)。
2、函数的两个顶点坐标分别在第一象限和第三象限,坐标为(√3a,√3a/3),(-√3a,-√3a/3)。
3、当a越大,图像的开口越大,曲线越向两坐标轴靠近。
4、根据定义域和图像性质,函数的值域为非零实数,即为:(-∞,0)∪(0,+∞)。