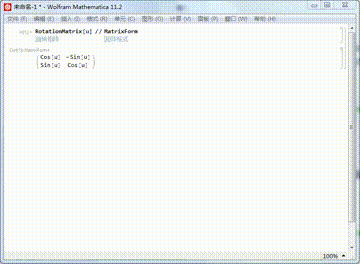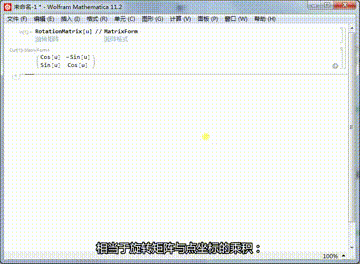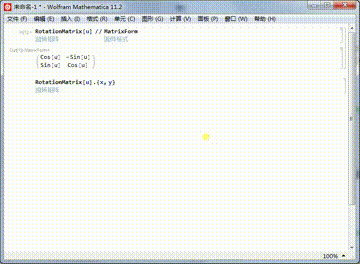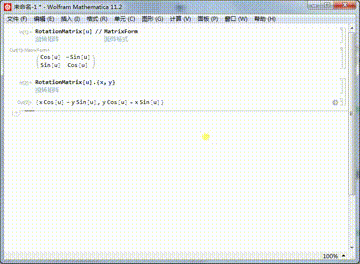
1、首先需要指出,二维空间里面,默认的旋转,都以原点为旋转中心。平面上绕原点旋转u,对应的旋转矩阵是:RotationMatrix[u]
2、平面上某个点{x,y},绕着原点旋转u,相当于旋转矩阵与点坐标的乘积:RotationMatrix[u].{x,y}
3、三维空间里面,绕着x轴的旋转,可以表示为:RotationMatrix[u, {1,0,0}]注意,这时候,旋转中心已经不是原点了。
4、点{x,y,z}绕x蛹侦硫馕轴旋转u,得到的点的坐标可以写成:RotationMatrix[u, {1,0,0}].{x,y,z}你会发现,旋转前后,点的x坐标不变。
5、设直线l经过原点,和点{x,y,z},那么,绕直线l的旋转,就可以写成:RotationMatrix[u, {x,y,z}]
6、上面这个矩阵很复杂,我尺攵跋赈们需要指定,x,y,z都是实数。FullSimplify[Refine[RotationMatrix[u, {x, y, z}], Element[{x, y, z魈胺闹臣}, Reals]] /. {Abs[x]^2 -> x^2, Abs[y]^2 -> y^2, Abs[z]^2 -> z^2}]