1、根据函数特征,函数自变量可以取全体实数,即定义域为:(-∞,+∞),并根据定义域和因式分解,判断函数3x^3+y^3=4x的取值正负。
2、定义域是指该函数的有效范围,函数的定义域就是使得这个函墙绅褡孛数关系式有意义的实数的全体构成的集合。 形剧安颌儿如y=f(x),则x是自变量,它代表着函数图像上每一点的横坐标,自变量的取值范围就是函数的定义域。f是对应法则的代表,它可以由f(x)的解析式决定。
3、函数的单调性,通过函数的一阶导数,求出函数驻点,由一阶导数的正负,判断函数的单调性,进而得到函数3x^3+y^3=4x的单调区间。
4、 函数单调性是针对某一个区间而言的,是一个局部性质。因此,说单调性时最好指明区间。有些函数在整个定义域内是单调的;有些函数在定义域内的部分区间上是增函数,在部分区间上是减函数;有些函数是非单调函数,如常数函数。
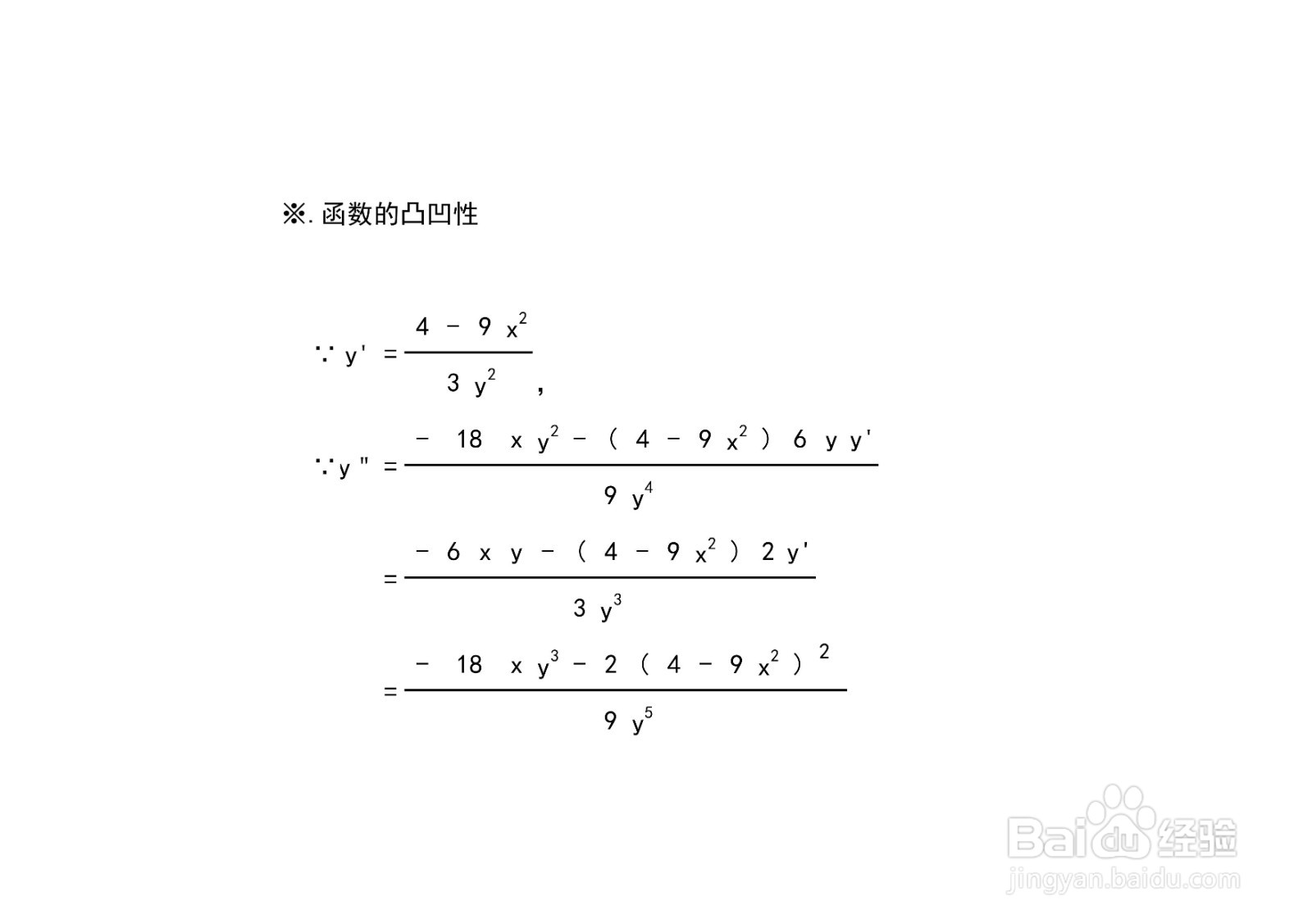
5、函数的凸凹性,通过函数3x^3+y^3=4x的二阶导数,解析函数3x^3+y^3=4x的凸凹性。
6、几何的直观解释:如果一个函数f(x)在某个区间I上有f'&拭貉强跳#39;(x)(即二阶导数)>0恒成立,那么在区间I上f(x)的图像上的任意两点连出的一条线段,唁昼囫缍这两点之间的函数图像都在该线段的下方,反之在该线段的上方。
7、函数的奇偶性,根据奇函数的判断原则,知函数图像关于原点对称,即函数为奇函数。
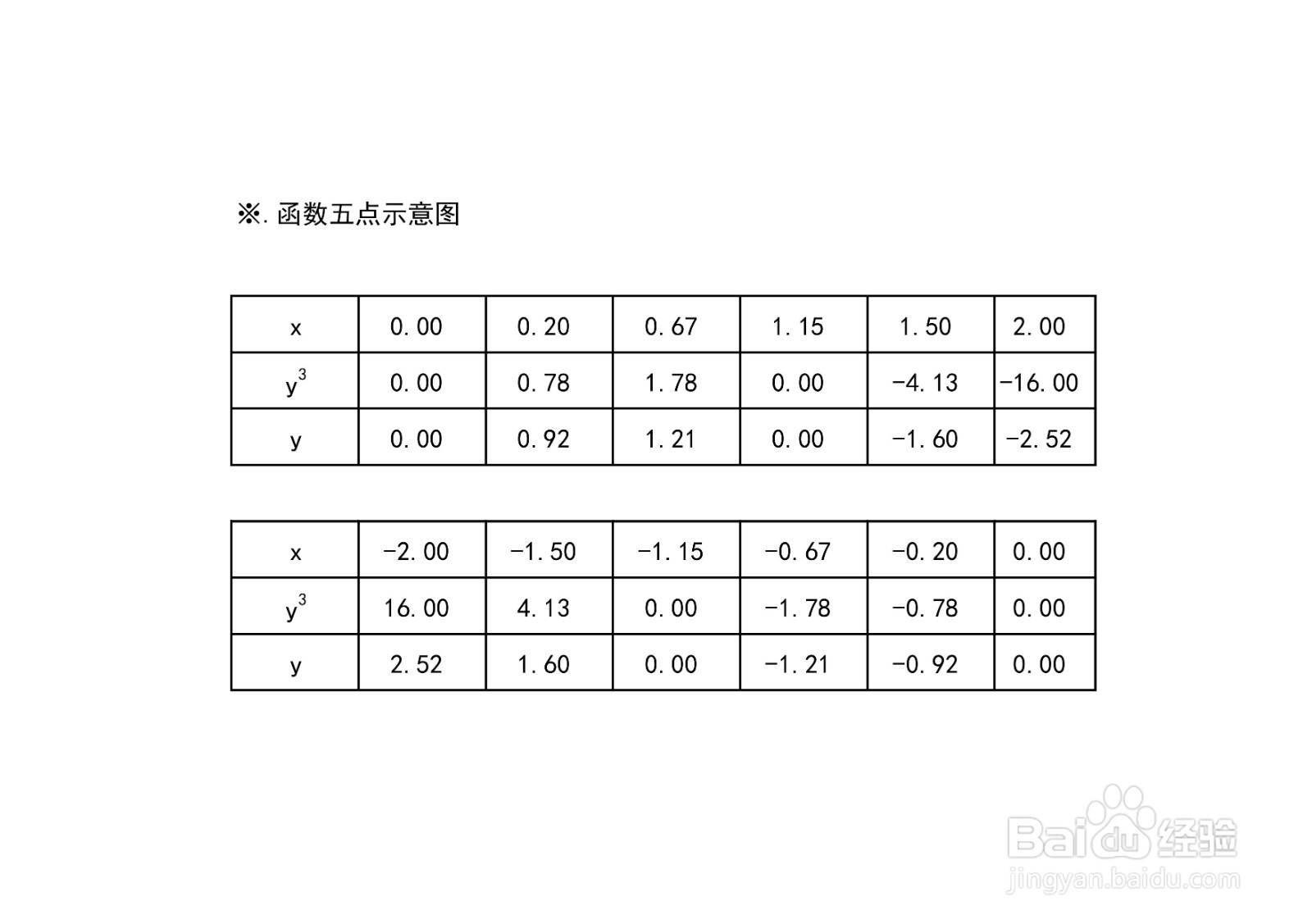
8、函数五点图,列举隐函数3x^3+y^3=4x上部分点图表,归纳如下表所示:
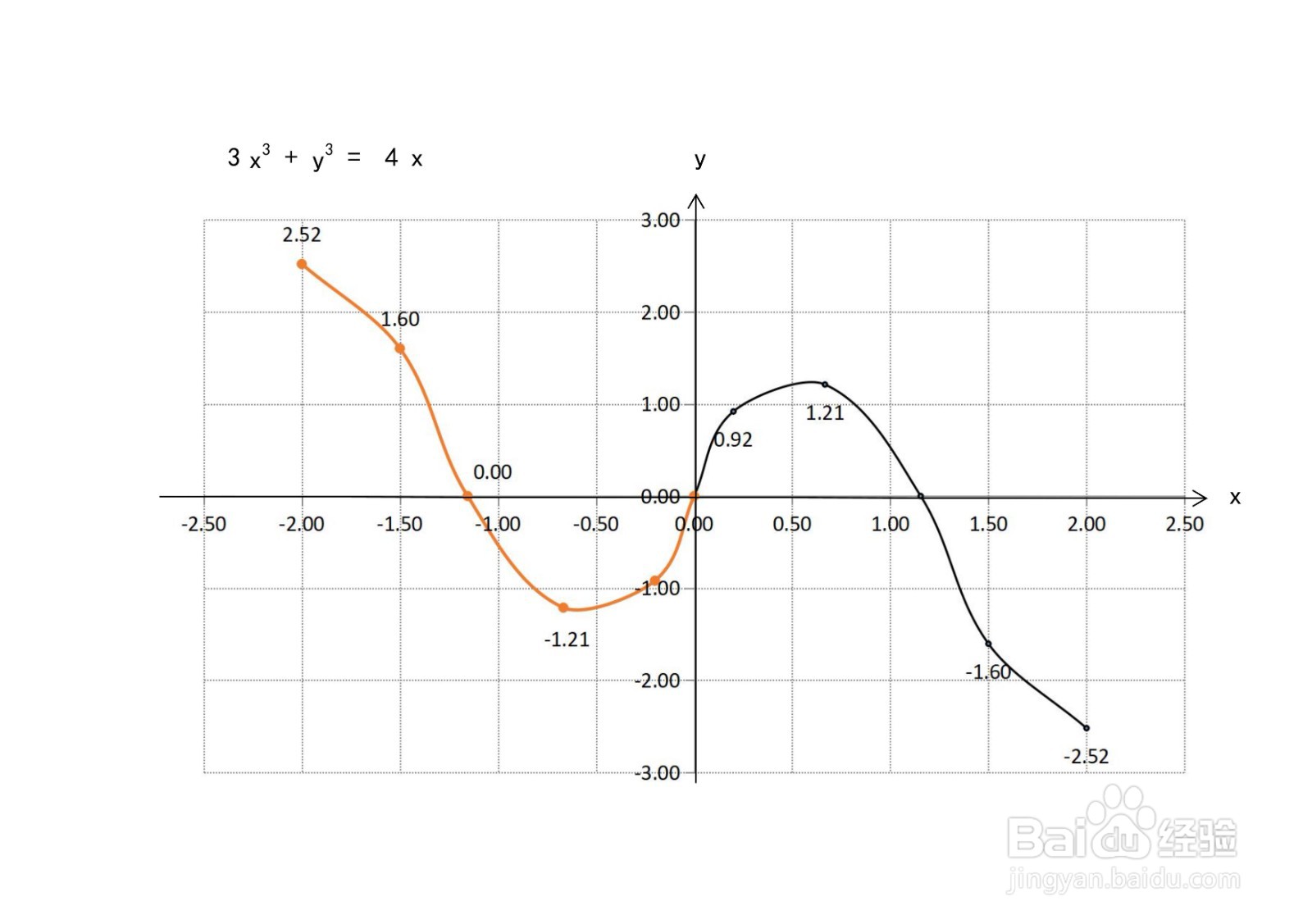
9、函数的示意图,综合以上函数3x^3+y^3=4x的定义域、值域、单调性、凸凹性、奇偶性等性质,函数的示意图如下: