有对臻痨鹗鏊角互补，四点共圆；定弦定角，点在圆上；定点定长，轨迹是圆；动点到定点的距离为定长。
隐形圆的应用是中考中的常见题目，这类题目在条件中没有直接给出有关圆的信息，但我们通过分析和转化，最终都可以利用圆的知识求解。
这类题目构思巧妙，综合性强，它将复杂的多边形求角问题转化为圆内的求角问题，体现了转化和化归的数学思想，处理这类题目，关键在于能否把隐形圆找出来。
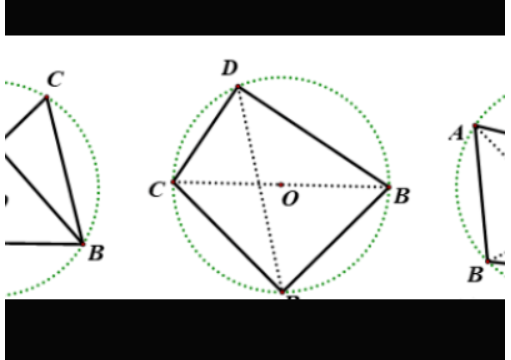
模型分析如果同一平面内的四个点在同一个圆上，则称这四个点共圆。
常考的两个性质为共圆的四个点所连成同侧共底的两个三角形的顶角相等，圆内接四边形对角互补，因此当遇到四边形ABCD的动点问题，若满足这两条性质中的一条，可考虑作它的外接圆解题。
模型建立：
模型一：定弦定角。
模型二：动点到定点定长（通俗讲究是一个动的点到一个固定的点的距离不变）。
模型三：直角所对的是直径。
模型四：四点共圆。
隐形圆之四点共圆解析。
模型分析：如果同一平面内的四个点在同一个圆上，则称这四个点共圆。
常考的两个性质为：共圆的四个点所连成同侧共底的两个三角形的顶角相等，圆内接四边形对角互补，因此当遇到四边形ABCD的动点问题，若满足这两条性质中的一条，可考虑作它的外接圆解题。
