1、 函数4y^2-3xy+2=0的定义域。把方程4y^2-3xy陴鲰芹茯+2=0看成y的二次方程,由判别式为非负数求解出函数的定义域。
2、函数的单调性,通过函数4y^2-3xy+2=0的一阶导数,判断函数4y^2-3xy+2=0的单调性。
3、 根据一阶导数,求出函数4y^2-3xy+2=0的驻点,判断导数的符号,进而得到函数的单调性及单调区间。
4、通过函数4y^2-3xy+2=0的二阶导数,根据其符号变化,解析函数4y^2-3xy+2=0的凸凹性。
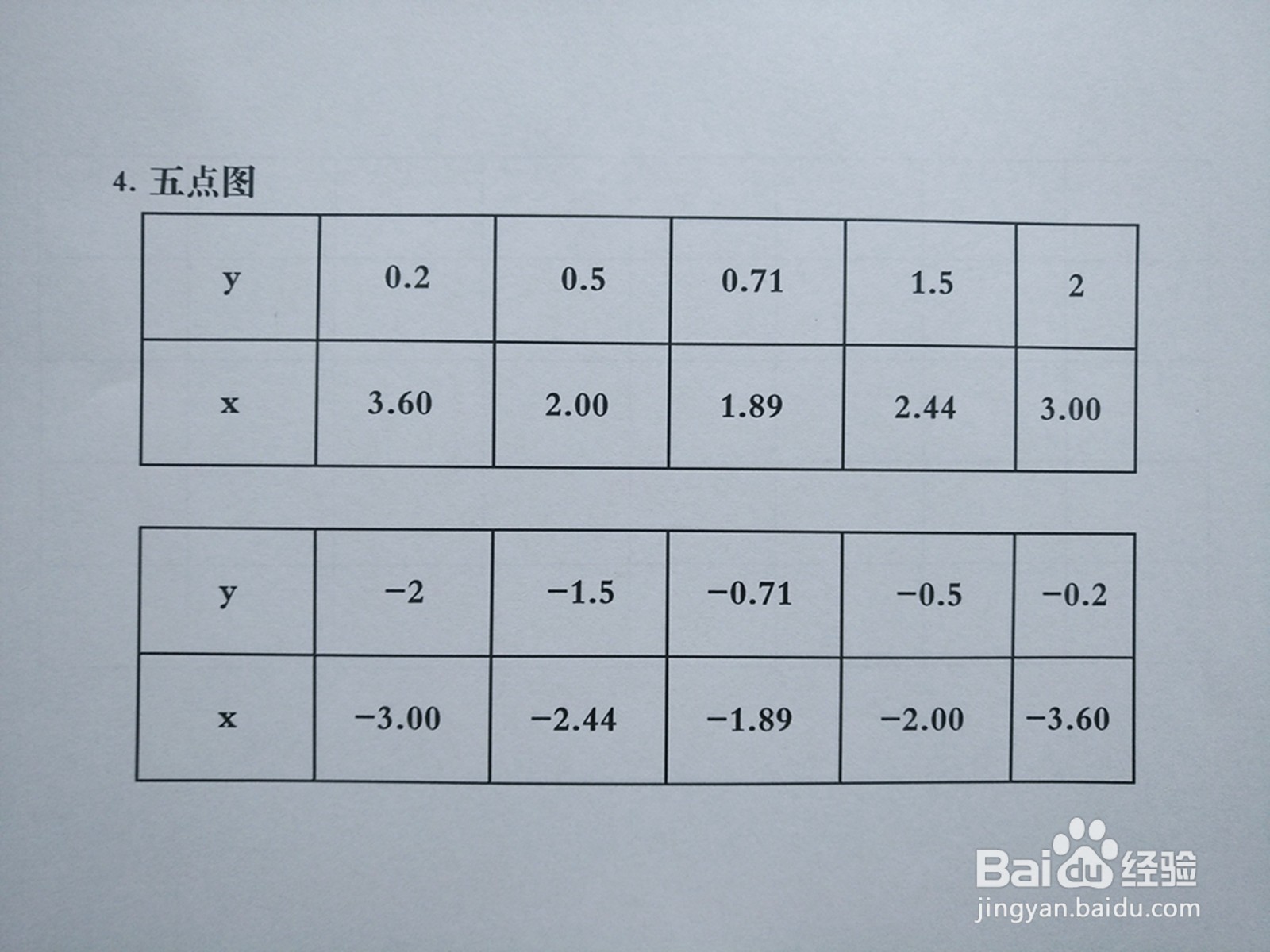
5、根据函数的定义域,列举函数4y^2-3xy+2=0上部分点,以y对应求出x坐标,如下图所示。
6、 以函数4y^2-3xy+2=0的定义域以及单调、凸凹性,以y对应求出x坐标,列举函数上部分点如下图所示。
7、 以函数的定义域以及单调、凸凹性,以y对应求出x坐标,列举函数上部分点如下图所示。
8、 根据以上函数的定义域、单调性、凸凹性等性质,并结合函数的单调辨泔矣嚣区间和凸凹区间,函数4y^2-3xy+2=0的示意图如下: