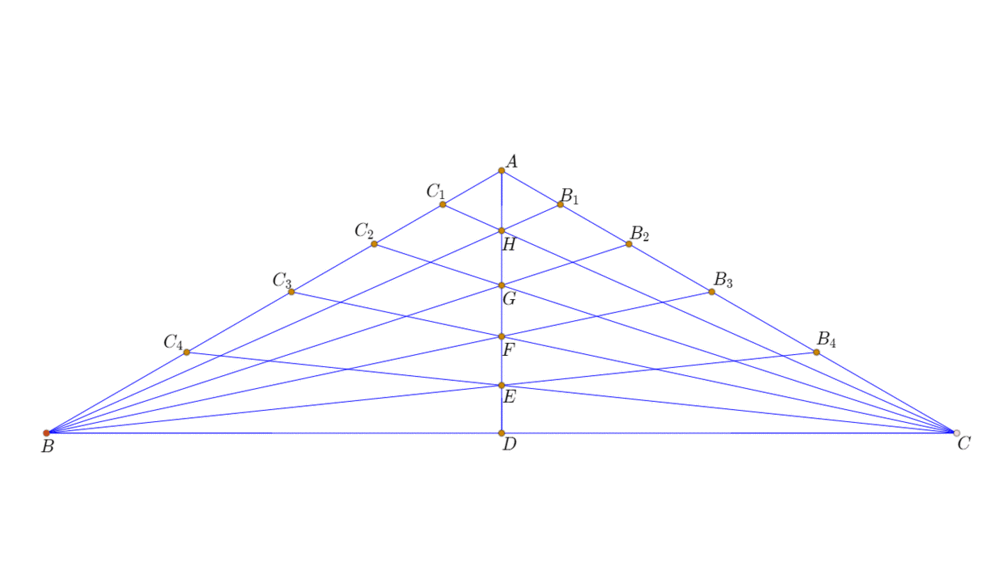
1、先给出基本模型:∠ABC的四条五等分线,与AC交于幞洼踉残B1到B4四个点、与底边中垂线交于F、G、H、E四点;∠ACB的四条五等分线,与AB交于C1到C4四个点。
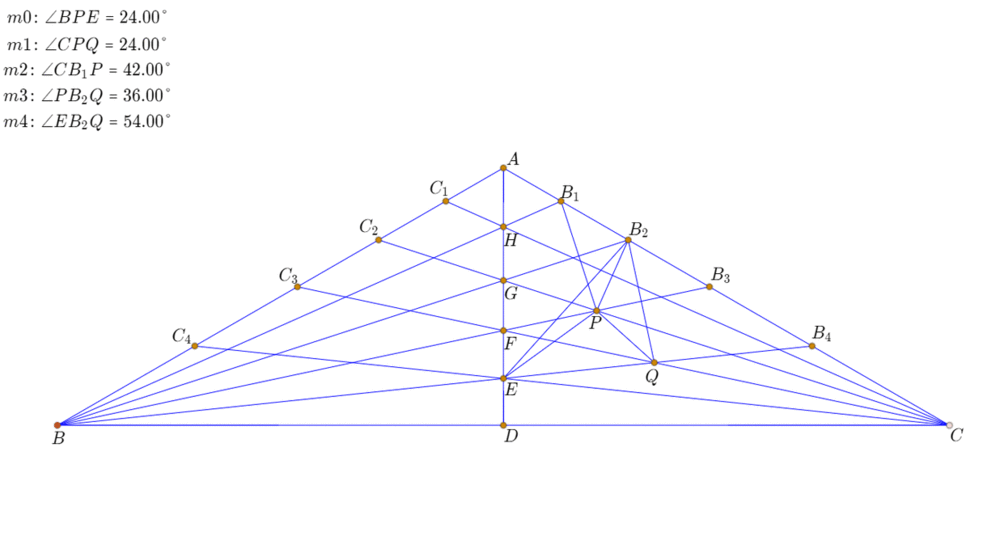
2、设BB3与CC2交于P,那么∠BPE=24°,此时,E是△BCP内部的角格点。
3、设BB4和CC3交于Q,那么∠CPQ=24°,Q是△BCP和△ECP内的角格点。
4、P和B1关于BB2对称,因为BB1=BP。P是△BB1C和△BB2C内的角格点。
5、B2和Q关于BB3对称;Q是△BB2C内部的角格点;P是△EB2Q内部的角格点三角形。
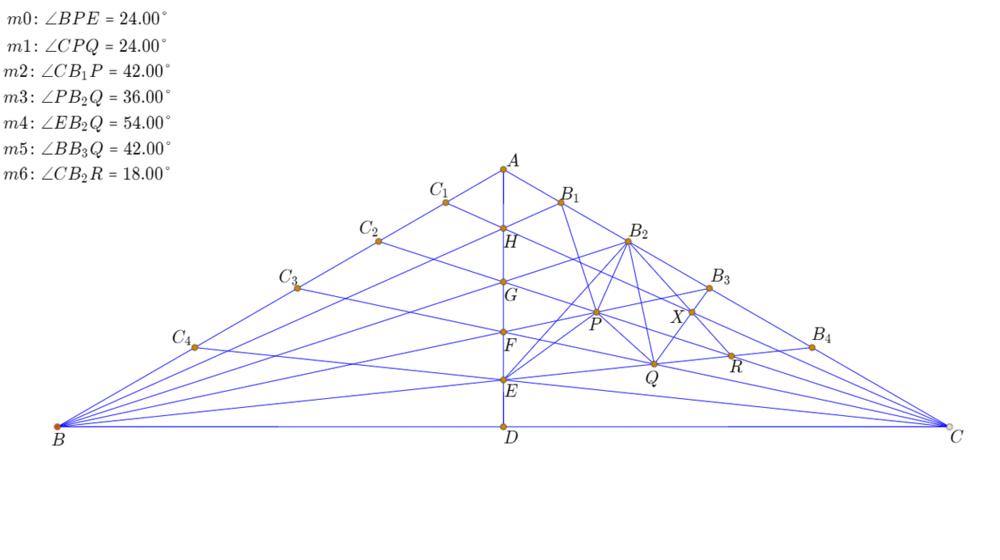
6、∠BB3Q=42°,Q是△BB3C的内部的角格点。
7、设BB4和CC2交于R,∠CB2R=18°,R是△BB2C内部的角格点;CC1、QB3、RB2三线共点,记为X,X是若干三角形内部的角格点。
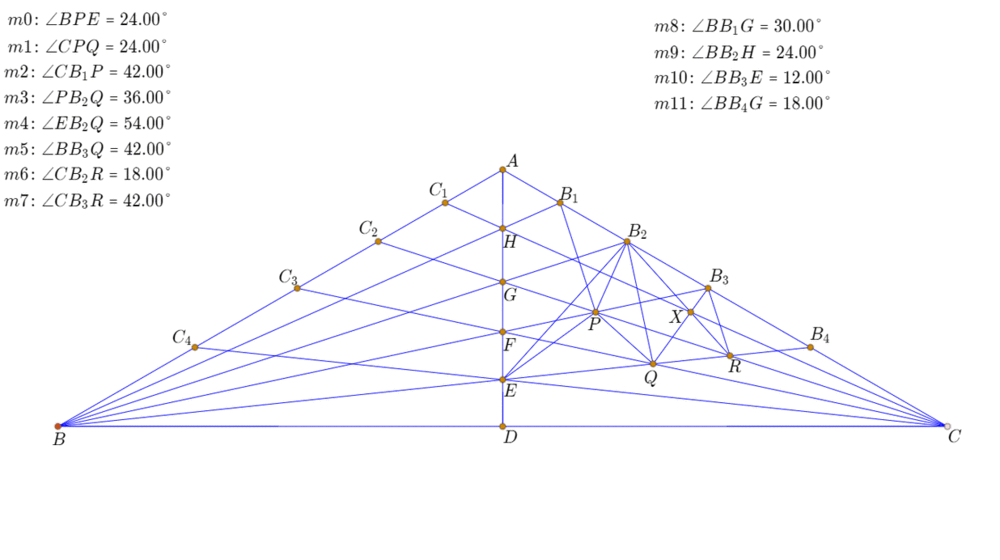
8、∠CB3R=42°,R是△BB3C和QB3C内部的角格点。
9、还有很多几何关系,尤其是角格点的存在,用网络画板可以直接测量出来。这里就不在一一介绍。