1、第一,平抛运动的方程如下图,包括垂直运动(垂直方向为自由落体运动)和水平匀速运动。
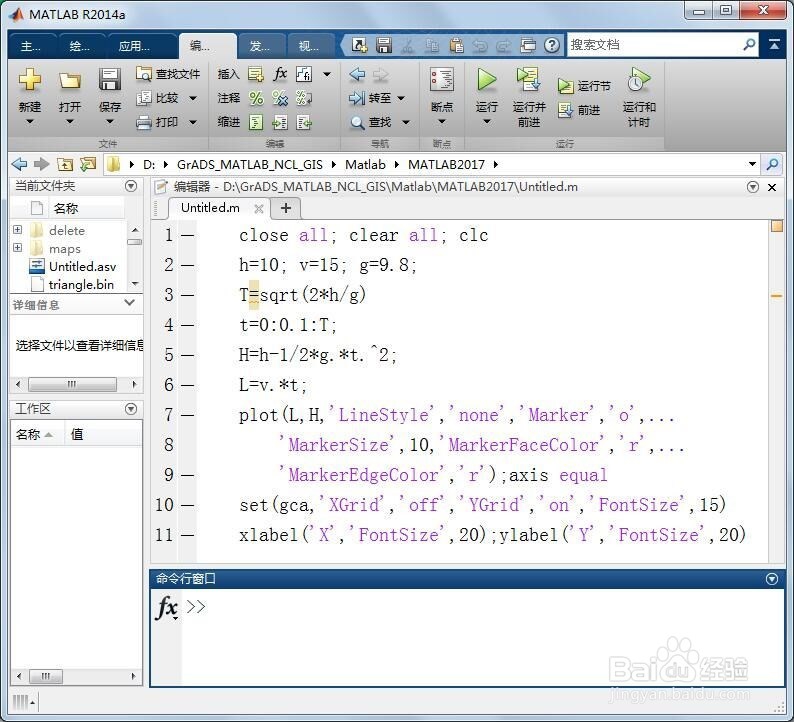
2、第二,启动MATLAB,新建脚本(Ctrl+N),输入以下代码:close all; clear all; 艘早祓胂clch=10; v=15; g=9.8;T=sqrt(2*h/g)t=0:0.1:T;H=h-1/2*g.*t.^2;L=v.*t;plot(L,H,'LineStyle','none','Marker','o',...'MarkerSize',10,'MarkerFaceColor','r',...'MarkerEdgeColor','r');axis equalset(gca,'XGrid','off','YGrid','on','FontSize',15)xlabel('X','FontSize',20);ylabel('Y','FontSize',20)
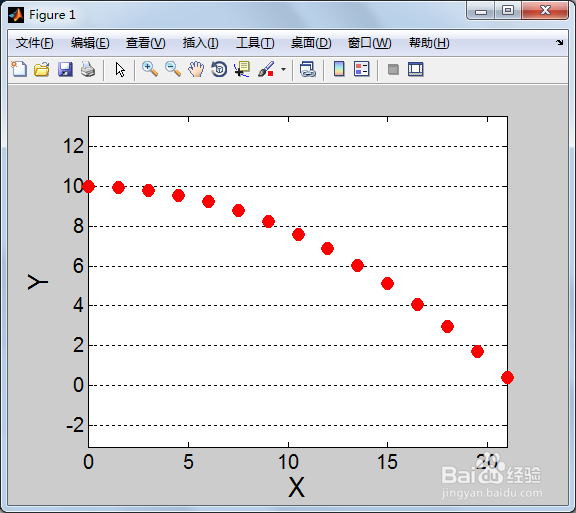
3、第三,保存和运行上述脚本,在命令行窗口(Command Window)得到T=sqrt(2*h/g)=1.4286,也就是说在h=10m的高度做平抛运动,物体落地所需的时间为1.4286秒。同时得到如下平抛运动轨迹图。
4、第四,将脚本中v=15改为5,也就是说平抛时的初始水平速度由15m/s改为5m/s,其他参数都不变。
5、第五,保存和运行上述脚本,在命令行窗口(Command Window)得到T=sqrt(2涯箨唁峦*h/g)=1.4286,也就是说在h=10m的高度做平抛运动,无论平抛时的初始水平速度如何懈吡赜痖变化,物体落地所需的时间不变,始终为1.4286秒。但是平抛的轨迹图有所变化(如下图,落地时水平运行距离变小)。