1、解析函数的定义域,结合对数函数的性质,要求真数为正数,即可求解函数y=ln(16/38+36x^2/73)的定义域。
2、函数的单调性,通过函数的一阶导数,求出函数y=ln(16/38+36x^2/73)的单调区间。
3、函数的单调性是函数的重要性质,反映了随着自变量的增加函数值的变化趋势,它是研究函数性质的有力工具,在解决比较大小、解决函数图像、值域、最值、不等式问题都有很重要的作用。
4、计算函数y=ln(16/38+36x^2/73)的二阶导数,得到函数的拐点,进而解析函数的凸凹性性并计算函数的凸凹区间。
5、由函数奇偶性判断原则,可判断函数为偶函数,图像关于y轴对称,并计算函数的极限。
6、解析函数y=ln(16/38+36x^2/73)五点图表,函数部分点解析表如下:
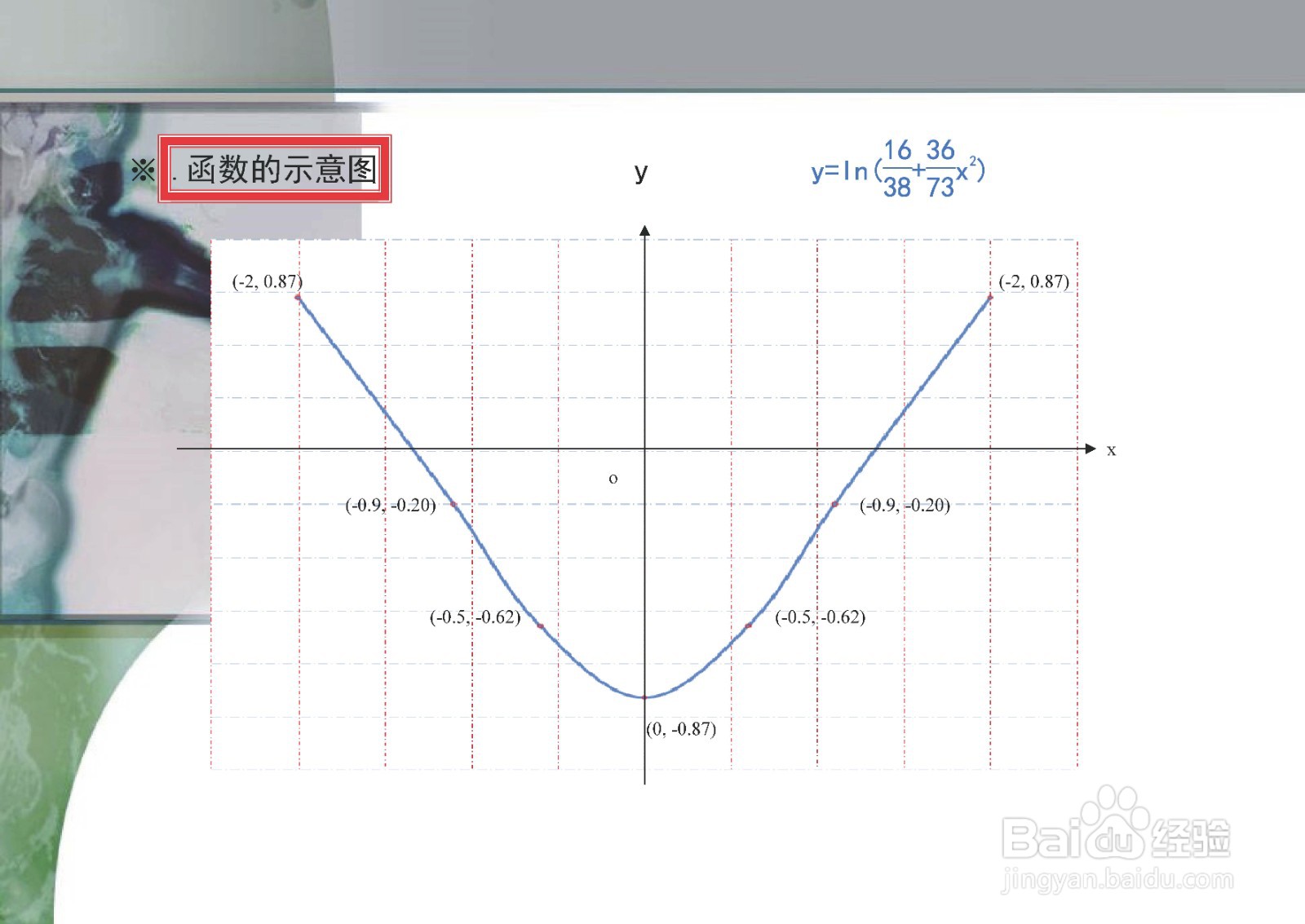
7、根据以上函数的定义域、单调性、凸凹、极限和奇偶等性质,并结合函数的驻点和拐点,即可画出函数y=ln(16/38+36x^2/73)的示意图如下。