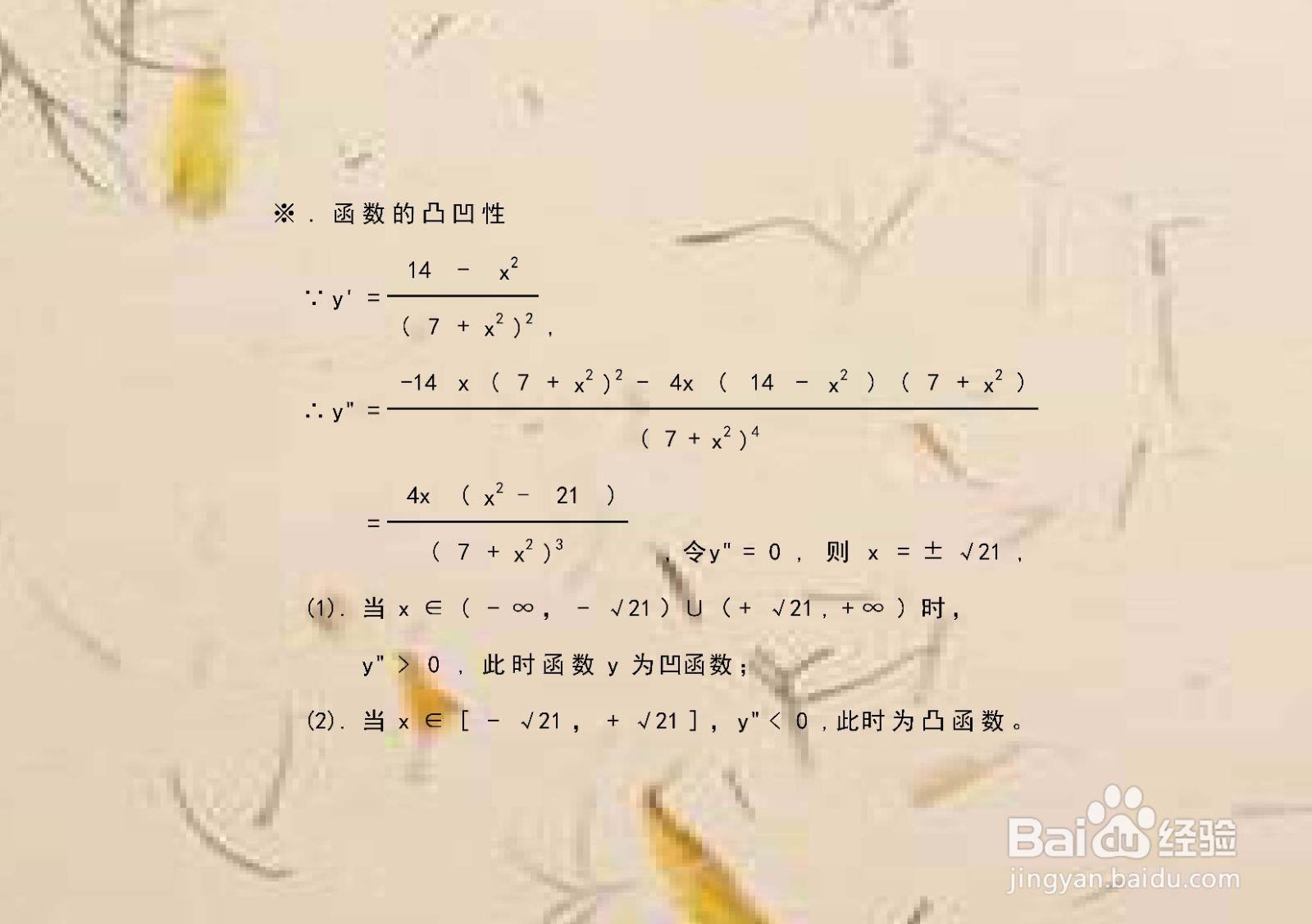1、函数为分式函数,函数分母不为0,并可求得函数自变量可以取全体实数。
2、定义域是指该函数的有效范围,函数的定义域就是使得这个函数关系式有意义的实数的全体构成的集合。
3、求出函数的一阶导数,并求出函数的驻点,判断函数一阶导数的符号,进而得到单调性和单调区间。
4、设f(x)在[a,b]上连续,在(a,b)内具有一阶导数,那么:(1)若在(a,b)内f'(x)>0,则f(x)在[a,b]上的图形单调递增;(2)若在(a,b)内f'(x)<0,则f(x)在[a,b]上的图形单调递减。
5、计算函数的二阶导数,进一步得函数的拐点,从而解析函数的凸凹性和凸凹区间。
6、如果一个函数f(x)在某个区间I上有f''(x)(即二阶导数)>0恒成立,那么在区间I上f(x)的图象上的任意两点连出的一条线段,这两点之间的函数图象都在该线段的下方,反之在该线段的上方。
7、根据函数奇偶性判定原则,判断函数为奇函数,则图像关于原点对称。
8、根据函数的定义域,结合函数的单调性,求出函数在定义域端点即在无穷大处的极限。
9、设函数f(x),|x|大于某一正数时有定义,若存在常数A,对于任意ε>0,总存在正整数X,使得当x>X时,|f(x)-A|<ε成立,那么称A是函数f(x)在无穷大处的极限。
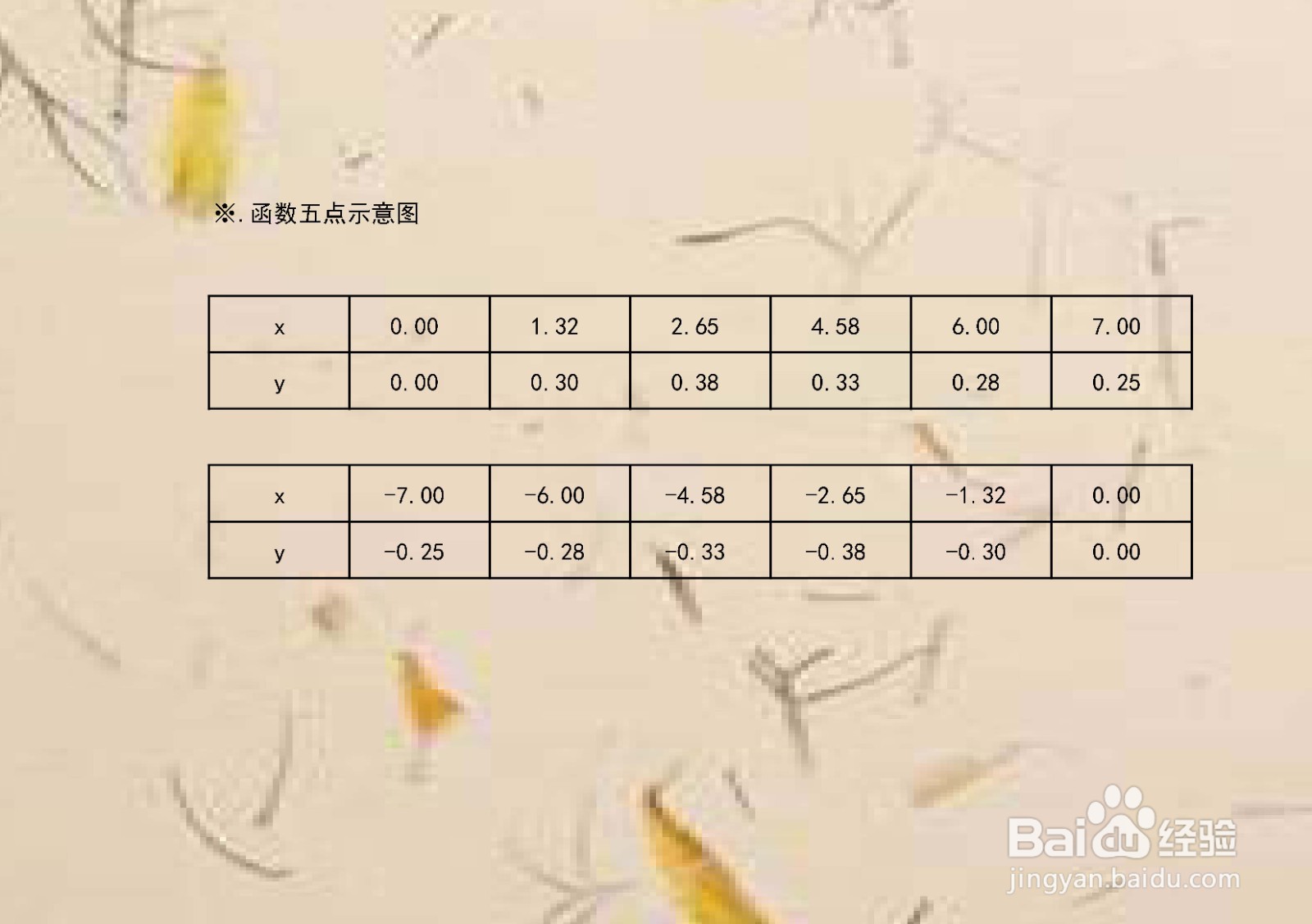
10、函数五点图,列表,函数部分点解析表如下:
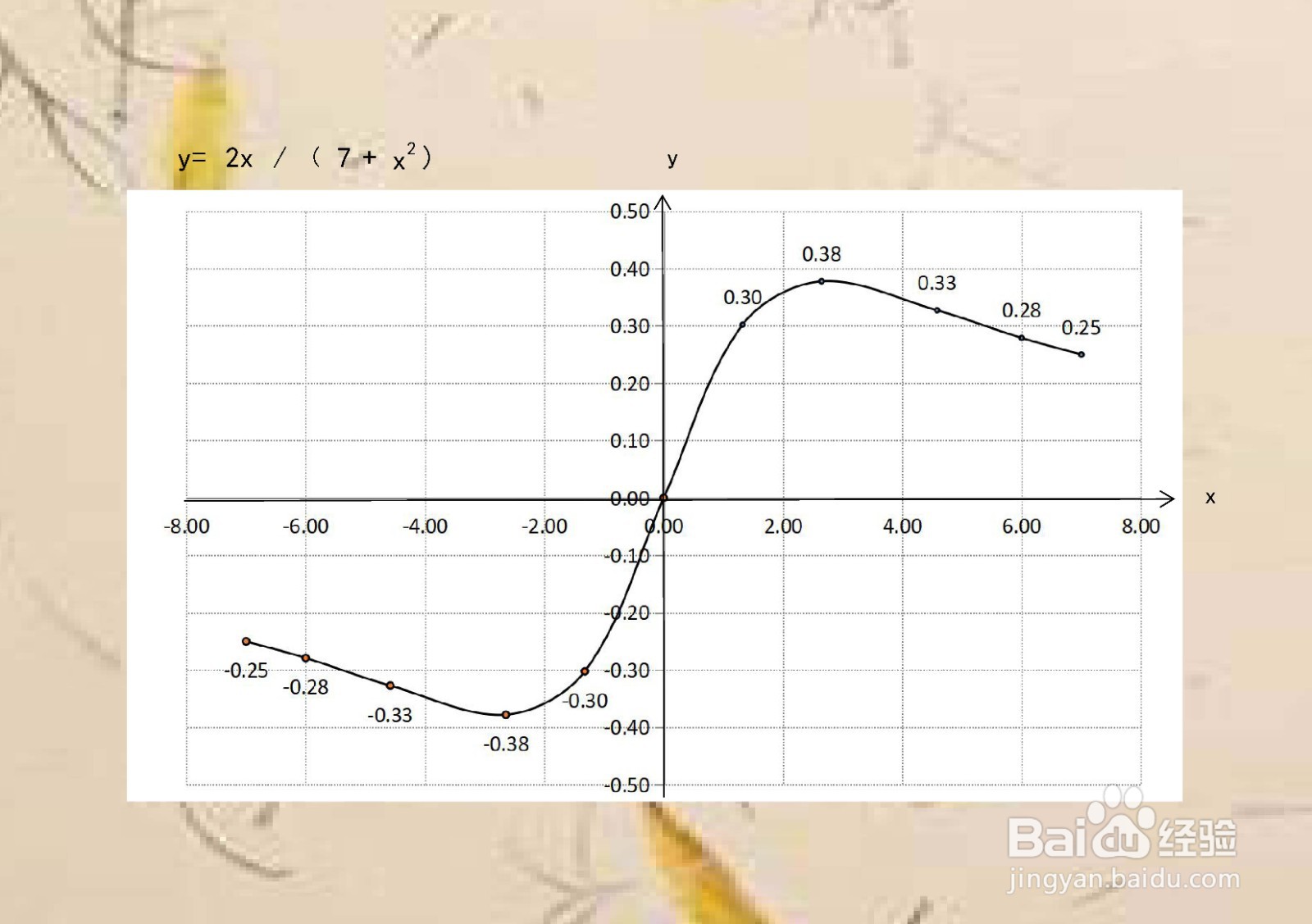
11、综合以上函数的定义域、值域、单调性、凸凹性、奇偶性以及极限等性质,函数的示意图如下。