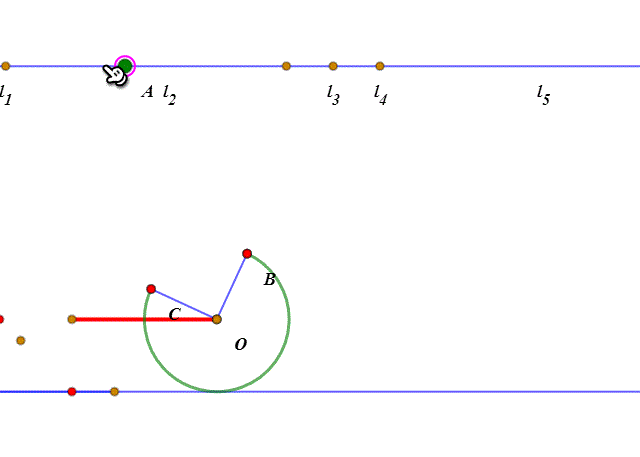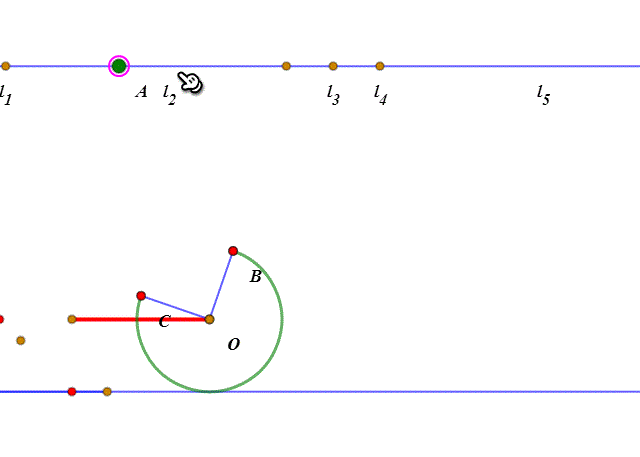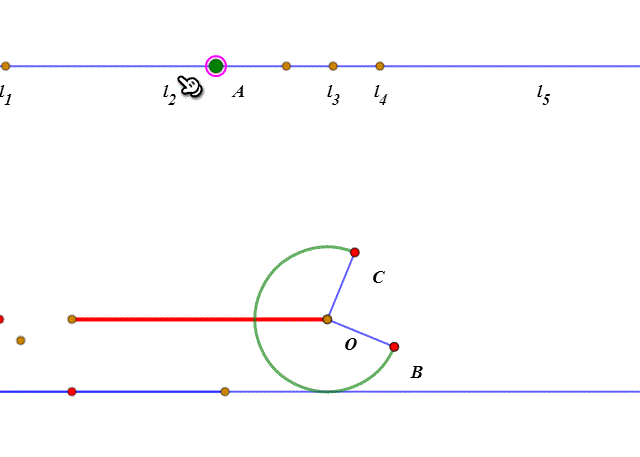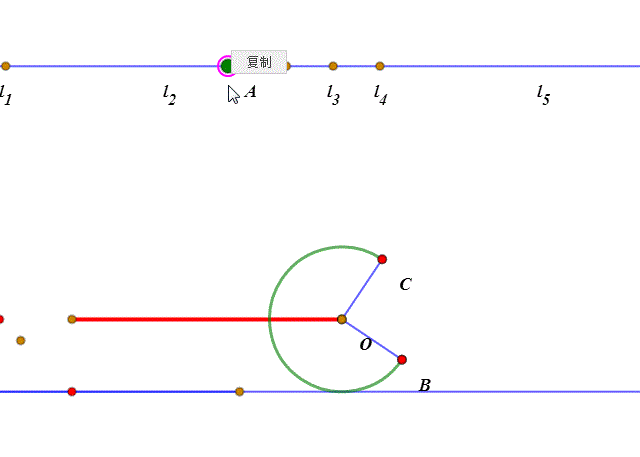
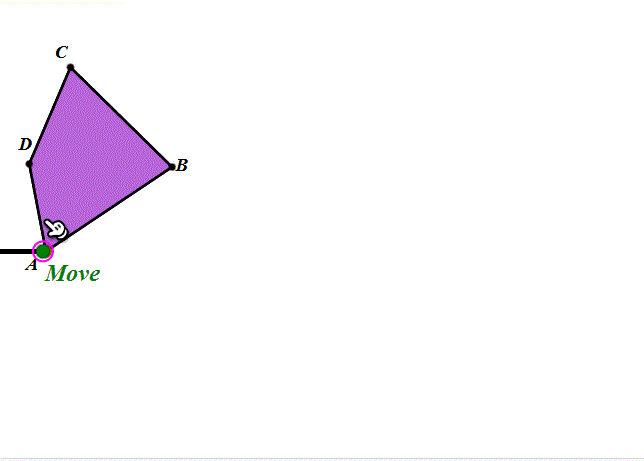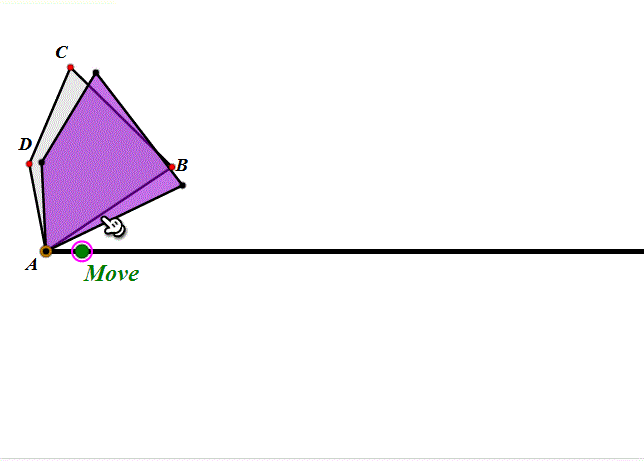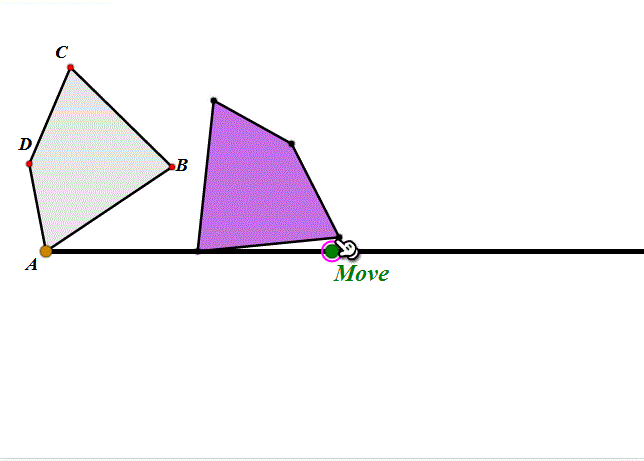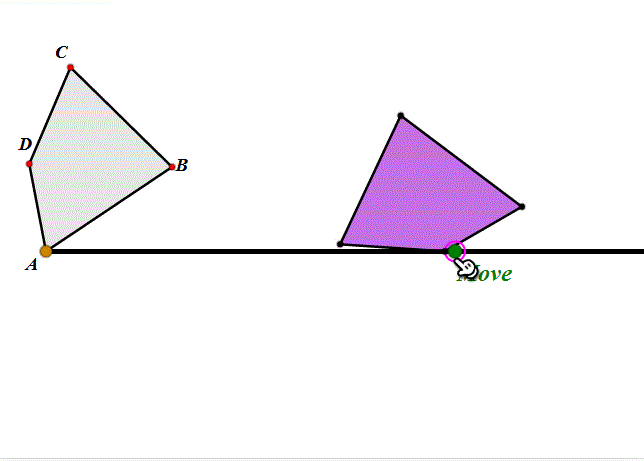
1、先来剖析一下这个滚动过程:当扇形开口朝下、BC处于撷渤猫辣水平状态的时候,所谓的“滚动”,其实就是整个扇形绕点C旋转45°。然后就是扇形的圆弧贴着直线滚动了。
2、圆弧的滚动,和圆的滚动的实现方法大同小异,都是“绕圆心旋转”和“圆心平移”。当“旋转”的弧长等于“平移”的距离,那么这就是“纯滚动”。
3、可以说,圆在直线上的滚动,就是旋转+平移。那么,其它图形在直线上的滚动会是怎样的呢?下图是任意四边形在圆上的滚动,其实就是依次绕着各顶点旋转。
4、等宽曲线在直线上的滚动,可以分解为若干个扇形的滚动。烂瘀佐栾这个多说无益,大家应该看课件,自己思考。至于更一般的情形,如:椭圆在直线上的滚动,三叶玫瑰线在直线上的滚动,等等,目前还没有网络画板的课件。
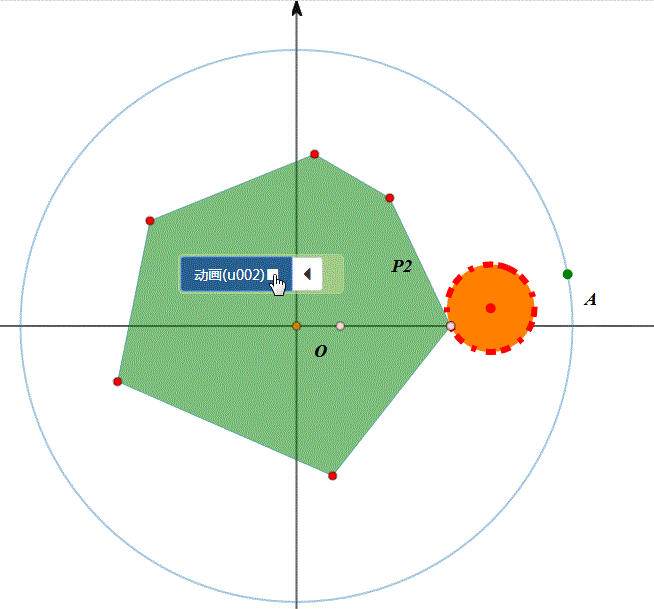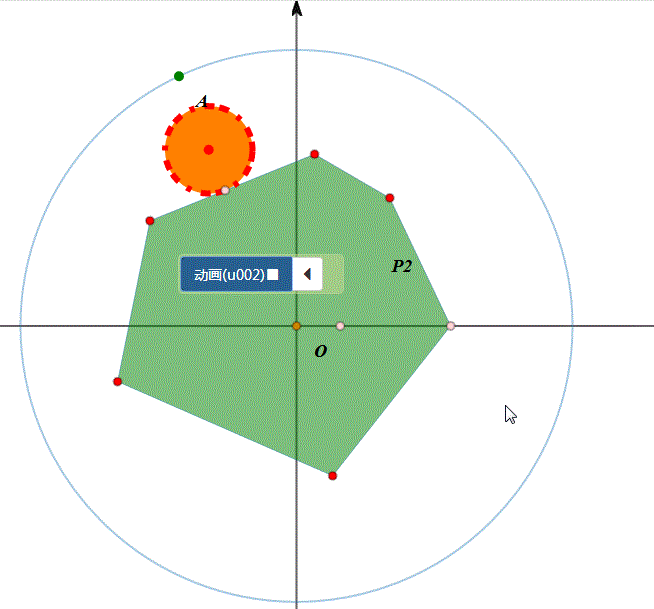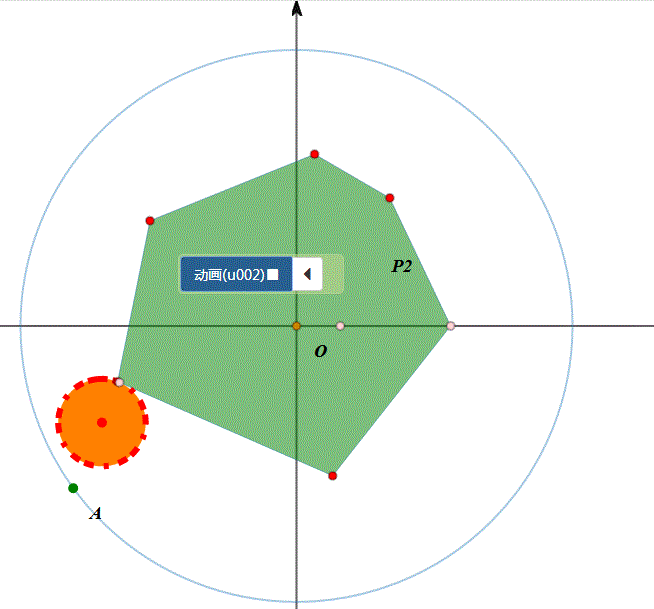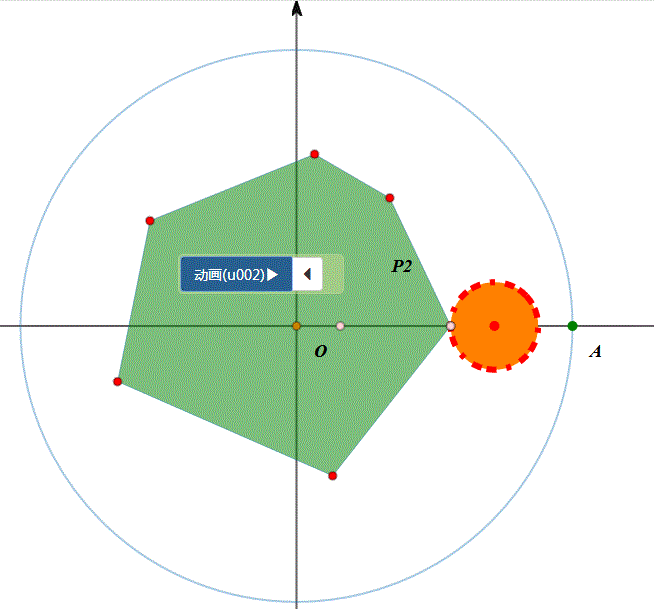
5、图形在圆上的滚动,分为两类:圆内、圆外。例如,圆在圆外的滚动,正多边形在圆内滚动……
6、我们考虑更一般的情形:给定某个图形,在另一条曲线上滚动,有没有办法实现统一模拟。