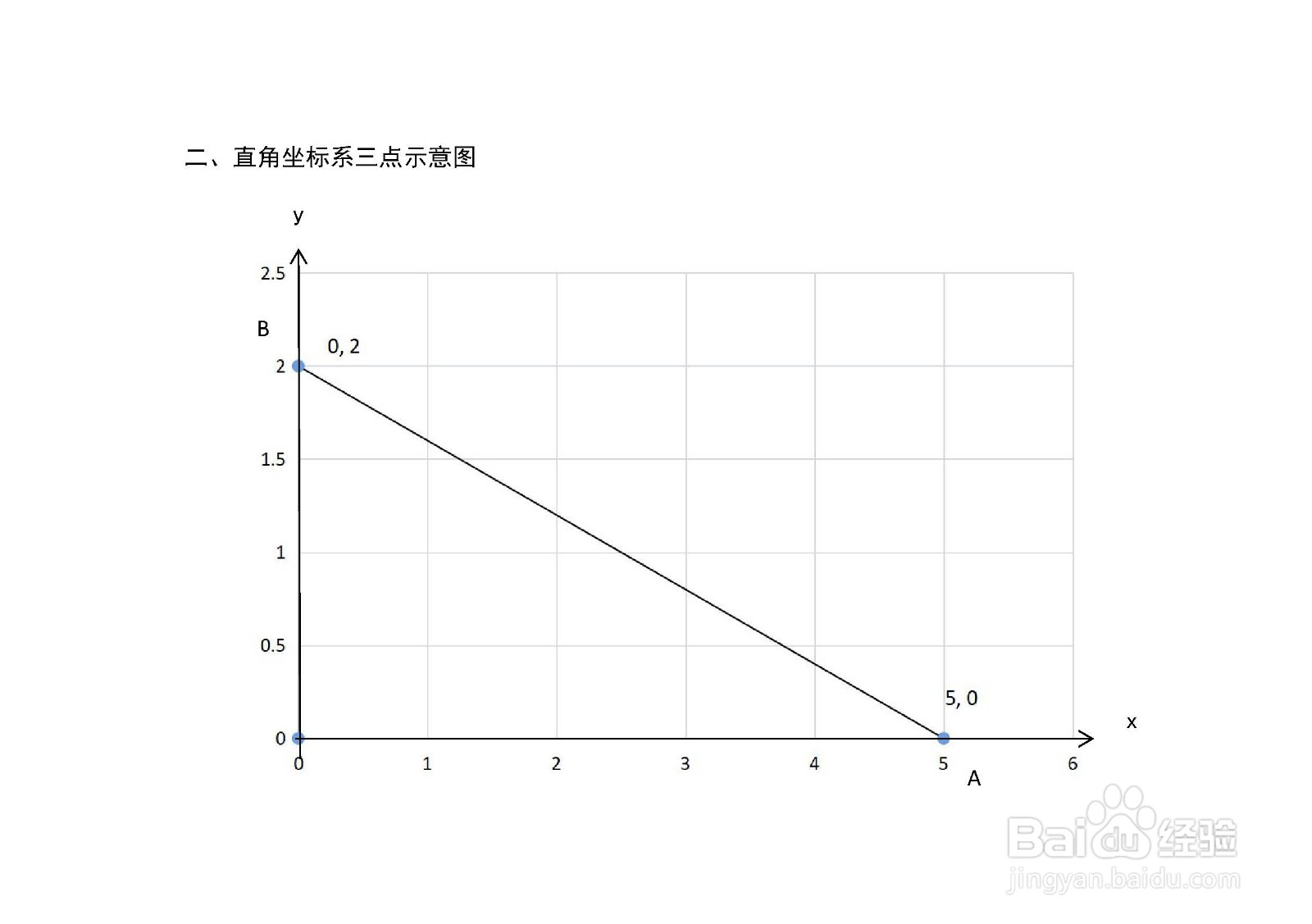
1、 直角三角形状的三个顶点坐标分别为:A(5,0),B(0,2),C(0,0),主要内容是介绍求构成的三角形的重心、内心、外心和垂心坐标的计算步骤。
2、由坐标系知识,在直角坐标中,将上述三个点进行描出。
3、直角三角形的两直角边AC,BC的长已知,再由两点距离公式,计算此时三角形的斜边AB的长。
4、重心的计算,三角形的重心即三条中线的交点,分别通过三个顶点与对边中点相连,中线的交点即是重心。
5、当三角形三个顶点分别为A(x1,y1),B(x2,y2),C(x3,y3),根据上述重心的定义,用定比分点求得:a=(x1+x2+x3)/3;b=(y1+y2+y3)/3。
6、垂心即三条高的交点,分别通过三个顶点作对边作垂线,垂线的交点即是垂心。对于本题,三角形为直角三角形,所以垂心即直角三角形的直角定点,故垂心为:H( 0 , 0 ).
7、该三角形的外心坐标计算,外心即外接圆的圆心,此时三角形三个顶点在圆上,圆心到三个顶点的距离相等,因此外心是三角形三条边的中垂线的交点。
8、 计算该直角三角内心坐标的主要思路:内心即内切圆的圆心,此时三角形三条边都与圆相切,圆心到三条边的距离相等,即内心到三角形三边的距离相等,因此内心是三角形三个角的角平分线交点。
9、 根据内心性质,本题设内心N的坐标为(m,n),当三角形三个顶点分别为A(x1,y1),B(x2,y2),C(x3,y3),由向量性质得aN帆歌达缒A+bNB+cNC=0: NA= ( x1-m , y1-n ) ;NB= ( x2-m , y2-n ) ;NC= ( x3-m , y3-n )。