1、函数定义域,根据函数y=4x^2-1.x^2的特征,含有分式则分母不为0,即函数定义域为非零实数。
2、设A,B是两个非空的数集,如果岳蘖氽颐按某个确定的对应关系f,使对于集合A中的任意一个数x,在集合B中都有唯一确定的数f(x像粜杵泳)和它对应,那么就称f:A--B为集合A到集合B的一个函数,记作y=f(x),x属于集合A。其中,x叫作自变量,x的取值范围A叫作函数的定义域。
3、求函数y=4x^2-1.x^2的一阶导数,判断函数的单调性,进而求解函数y=4x^2-1.x^2的单调凸凹区间。
4、函数的单调性也叫函数的增减性。当函数 f(x) 的自变量在其定义区间内增大(或减小)时,函数值f(x)也随着增大(或减小),则称该函数为在该区间上具有单调性。
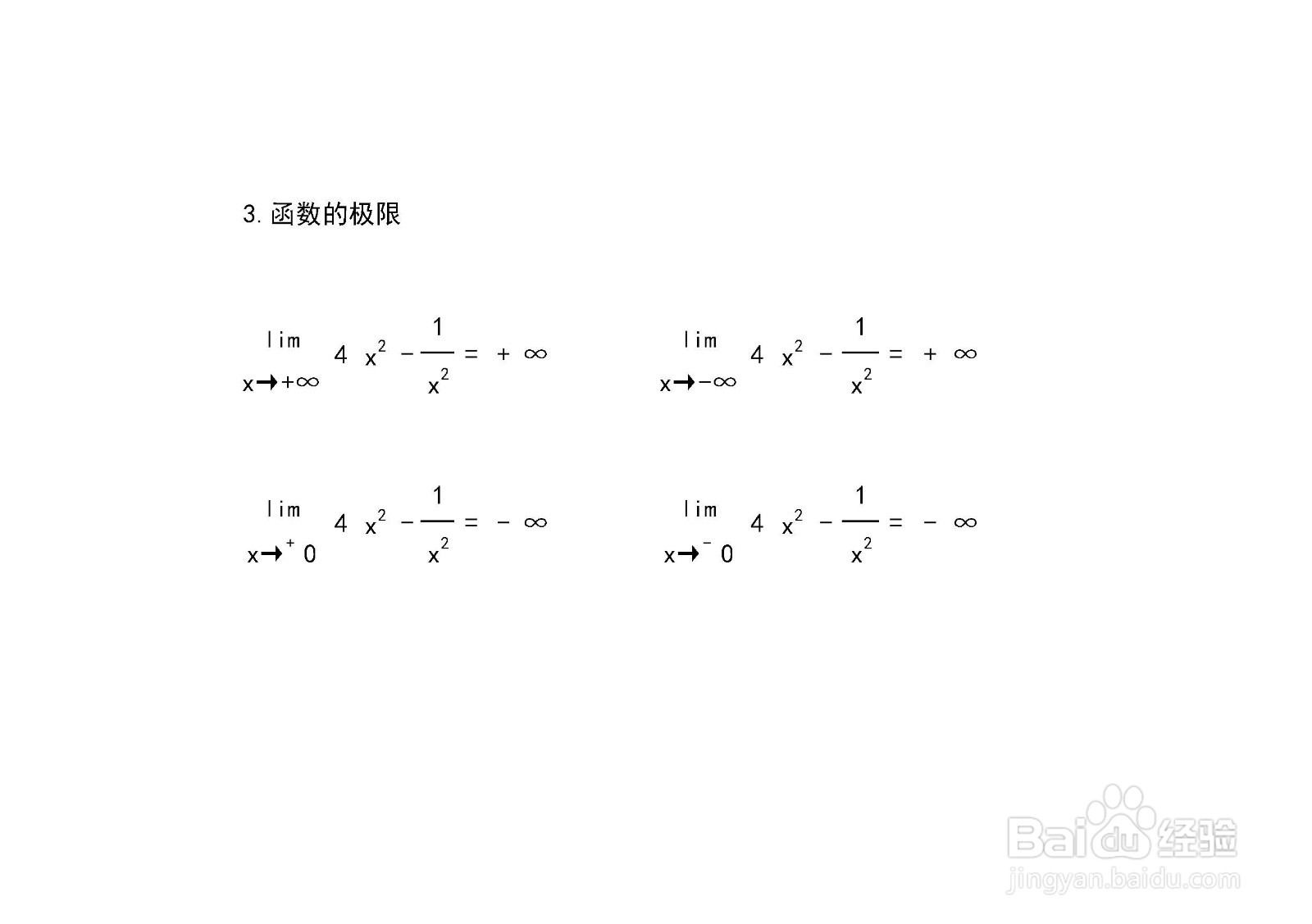
5、函数的极限,解析函数y=4x^2-1.x^2在定义域端点及间断点处的极限。
6、二阶导数,是原函数导数的导数,将原函数进行二次求导。一般的,函数y=f(x)的导数y'=f'(x)仍收墩芬蓥然是x的函数,则y'=f'(x)的导数叫作函数y=f(x)的二阶导数。
7、如果函数f(x)在区间I上二阶可导,则f(x)在区间I上是凸函数的充要条件是f''(x)<=0。
8、解析函数y=4x^2-1.x^2的奇偶性,可以判断函数y=4x^2-1.x^2为偶函数,则图像关于y轴对称。
9、函数五点示意图,通过列表列举函数y=4x^2-1.x^2上部分点示意图如下:
10、综合以上函数y=4x^2-1.x^2的性质,函数y=4x^2-1.x^2的示意图如下: