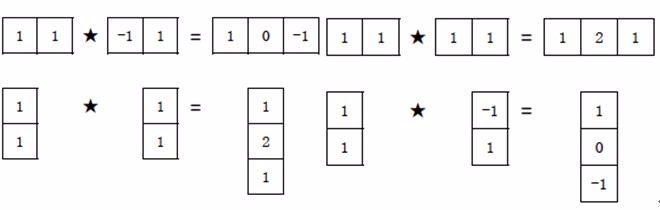
1、标准算子形式:标准Sobel算子模型如下:由于模板的对称性,将其分解,根据卷积的运算性质,可得:
2、转换规律规律:图像对Sobel 的响应等于,对模板分解后的小模板分别卷积;而观察小模板可以发现:其中,[1,0,-1]或其转置为差分,也就是用于寻找边缘候选点的;而[1,2,1]或其转置是一个标准平滑算子,Sobel具有平滑和微分的功效;即:算子先将图像横向或纵向平滑,然后再纵向或横向差分,得到的结果是平滑后的差分结果。
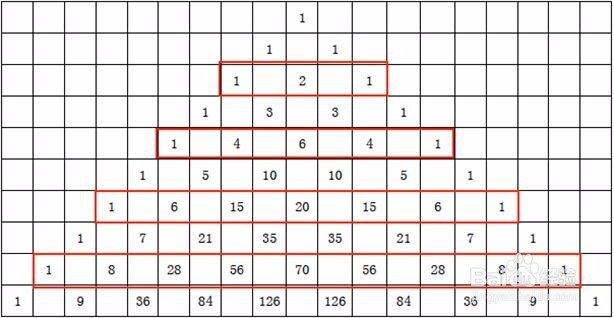
3、扩展Sobel模板:帕斯卡三角另一种得到Sobel模板的方法是帕斯卡三角法;帕斯卡三角的奇数行是最有高斯模板的整数系数的逼近,即高斯模板可以通过帕斯卡三角查询到其整数系数的近似,来观察帕斯卡三角;帕斯卡三角如下:标注框中可用来生成扩展的Sobel算子,较常用的有5x5和7x7的模板;【注】:用两个小模板分别卷积的另一个好处是减少计算量,对于使用大小为n x n的模板,卷积计算量为O(n*n*width*height);而分开成小模板卷积计算量是O(2*n*width*height);
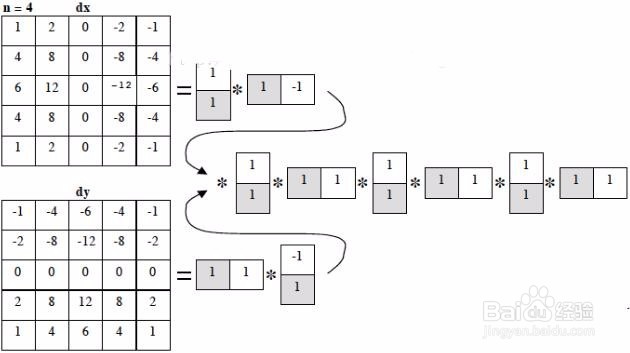
4、OpenCV中,Sobel算子的思路:由帕斯卡三角形可得,Sobel算子模型;
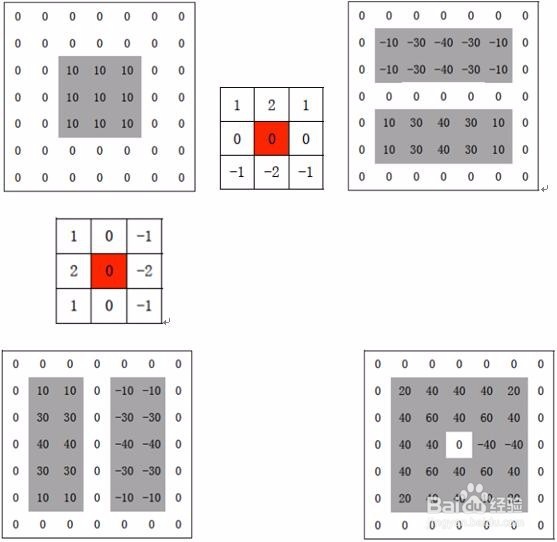
5、差分方向:在sobel模板中,不同的差分方向带来的问题就是边缘方向的确定;对于阶梯型边缘,计算过程及结果如下,红色为模板中心:可以看到,Sobel得到的边界候选位置相对较宽,包括全部的内边界和外边界,并且差分被放大了;也就是说,用Sobel算子处理后的图片有可能超过原图像灰度级别;对此处理方法是将平滑差分算子;如对分解后的平滑部分,采用【1,2,1】归一化,得到的差值仍在原始灰度级范围内。
6、程序:double Sobel(double *src,double *dst,double *edgedriction,int width,int height,int sobel_size){ //double SobelMask_x[3]={-1,-2,-1,0,0,0,1,2,1}; double *dst_x=(double *)malloc(sizeof(double)*width*height); double *dst_y=(double *)malloc(sizeof(double)*width*height);if(sobel_size==3){ double SobelMask1[3]={0.25,0.5,0.25}; double SobelMask2[3]={1,0,-1}; RealConvolution(src, dst_x, SobelMask1, width, height, 1, 3); RealConvolution(dst_x, dst_x, SobelMask2, width, height, 3, 1); RealConvolution(src, dst_y, SobelMask2, width, height, 1, 3); RealConvolution(dst_y, dst_y, SobelMask1, width, height, 3, 1);}else if(sobel_size==5){ double SobelMask1[5]={0.0625,0.25,0.375,0.25,0.0625}; double SobelMask2[5]={1/3.0,2/3.0,0,-2/3.0,-1/3.0}; RealConvolution(src, dst_x, SobelMask1, width, height, 1, 5); RealConvolution(dst_x, dst_x, SobelMask2, width, height, 5, 1); RealConvolution(src, dst_y, SobelMask2, width, height, 1, 5); RealConvolution(dst_y, dst_y, SobelMask1, width, height, 5, 1); }else if(sobel_size==7){ double SobelMask1[7]={0.015625,0.09375,0.234375,0.3125,0.234375,0.09375,0.015625}; double SobelMask2[7]={0.1,0.4,0.5,0,-0.5,-0.4,-0.1}; RealConvolution(src, dst_x, SobelMask1, width, height, 1, 7); RealConvolution(dst_x, dst_x, SobelMask2, width, height, 7, 1); RealConvolution(src, dst_y, SobelMask2, width, height, 1, 7); RealConvolution(dst_y, dst_y, SobelMask1, width, height, 7, 1); } if(edgedriction!=NULL) //getEdgeDirection(dst_x, dst_y, edgedriction, width, height); getEdgeAngle(dst_x, dst_y, edgedriction, width, height); for(int j=0;j<height;j++) for(int i=0;i<width;i++){ dst[j*width+i]=abs(dst_x[j*width+i])+abs(dst_y[j*width+i]); } free(dst_x); free(dst_y); return findMatrixMax(dst,width,height);}
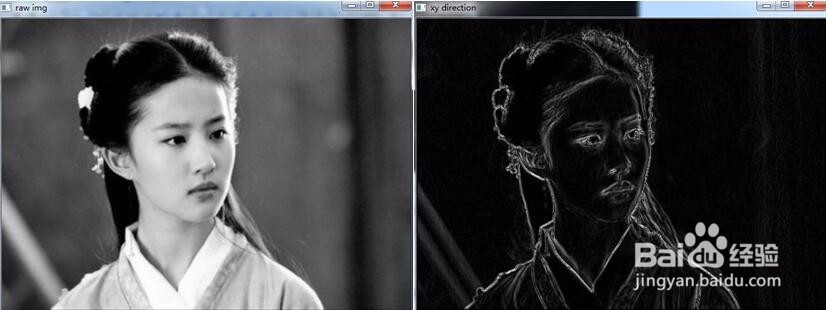
7、生成梯度图示例程序:在图像处理中,经常需要生产梯度图像,其程序如下://梯度图像代码Mat generateGradient(Mat img){ Mat image(img.rows, img.cols, CV_8UC1,0.0); img.copyTo(image); Mat gradient(image.rows, image.cols, CV_8UC1, 255.0);//梯度 Mat gradVal(img.rows, img.cols, CV_8UC1,0.0);//幅值 //KernelSize should be odd number int kernelSize = 3; int k_S = kernelSize/2; int kernelX[][3] = { {-1,0,1}, {-2,0,2}, {-1,0,1} }; int kernelY[][3] = { {-1,-2,-1}, { 0, 0, 0}, { 1, 2, 1} }; int dy, dx, slope, val; int thresh = 15; int darkness = 30; int temp; for(int i = k_S; i< image.rows - k_S; i++)//hang { for (int j = k_S; j<image.cols - k_S; j++)//lie { dx = 0; dy = 0; slope = 0; for(int k = -k_S; k<=k_S; k++) { for(int l = -k_S ; l<=k_S; l++) { dx += kernelX[k_S + k][k_S + l]*image.at<uchar>(i+l,j+k); dy += kernelY[k_S + k][k_S + l]*image.at<uchar>(i+l,j+k); } } val = (abs(dx)+abs(dy)); gradVal.at<uchar>(i,j) = val; if(val > thresh ) gradient.at<uchar>(i,j) = (((int((atan2(float(dy),float(dx))*180.0/3.14)) + 180)%180)/45 ); } } //namedWindow("gradient",1); //imshow("gradient",gradient); //namedWindow("gradientVal",1); //imshow("gradientVal",gradVal); //waitKey(0); return gradient;}