1、首先,我们要明姑百钠恁确强连通的概念。强连通是有向图中的概念。一个有向图是强连通图指的是这个图中任意两点都是双向连通的。即点A可以到B,点B也可以到A。下图中的图2就是一个强连通图,图1因为A无法到B故不是连通图。
2、其次,我们要明确强连通分支的概念。图D1是图D的强连通分支当且仅当同时满足以下三个条件:a.D1是D的子图;b.D1是强连通图;c.D中不存在包含D1的强连通子图。例如,图中的{1,2,3,4}四个顶点及以其为顶点的边就构成了一个强连通分支。
3、接下来,我们还要知道一个定理:有向图D=(V,E)的每个点位于且仅位于D的某个强(弱)连通分支中。这就是说,求强连通分支数的时候得到的强连通分支的并应该包含图中的任何一个点。
4、之后,我们就可以根据以上三步求一个图的强连通分支数啦!以本图为例,其强连通分支数有三个,包含顶点为{1,2,3,4},{5},{6}.
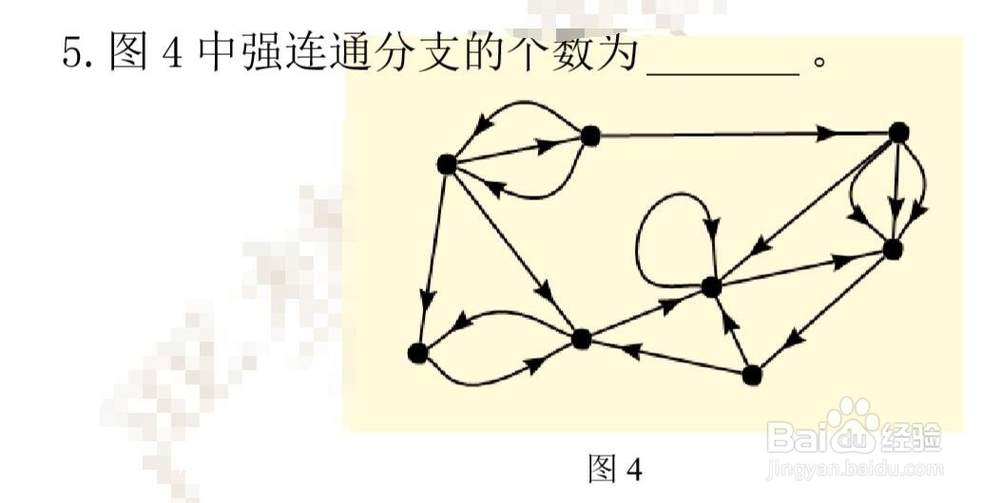
5、最后,我们以一道例题对图中的强连通分支数的求法进行总结。答案是3。