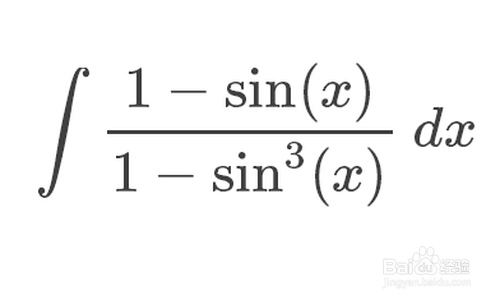1、我们要输入下图里面的公式,可以说比较容易:$$\Huge\int\frac{1-\sin(x)}{1-\sin^3(x)}\,dx$$
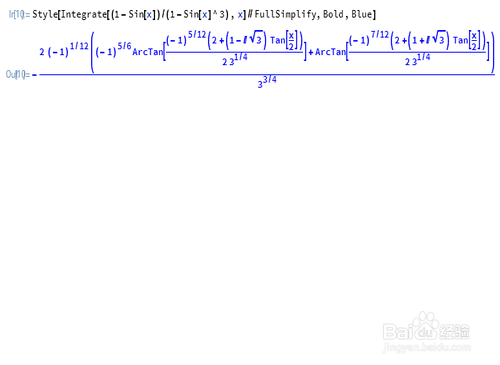
2、然后我们还要输入它的计算结果。先用Mathematica算一下结果是什么:Integrate[(1-Sin[x])/(1-Sin[x]^3),x]
3、这个式子长的不像话。然而我们可以用Mathematica把这个计算结果直接转化为TeXForm:Integrate[(1-Sin[x])/(1-Sin[x]^3),x]//TeXForm
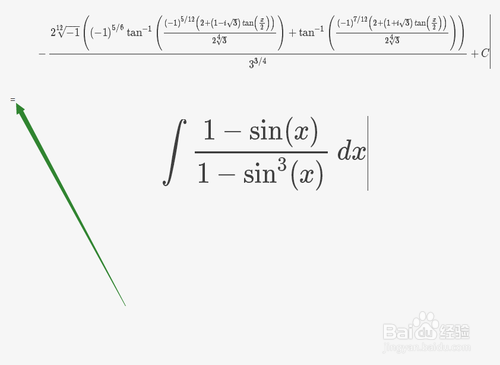
4、我们凸鹣沮北把这个运行结果复制到LaTeX编辑器(我在电脑上用的是CTex),在首尾各加上两个$,就可以得到想要的公式:$$-\frac{2\sqrt[12]撑俯擂摔{-1}\left((-1)^{5/6}\tan^{-1}\left(\frac{(-1)^{5/12}\left(2+\left(1-i\sqrt{3}\right)\tan\left(\frac{x}{2}\right)\right)}{2\sqrt[4]{3}}\right)+\tan^{-1}\left(\frac{(-1)^{7/12}\left(2+\left(1+i\sqrt{3}\right)\tan\left(\frac{x}{2}\right)\right)}{2\sqrt[4]{3}}\right)\right)}{3^{3/4}}+C$$
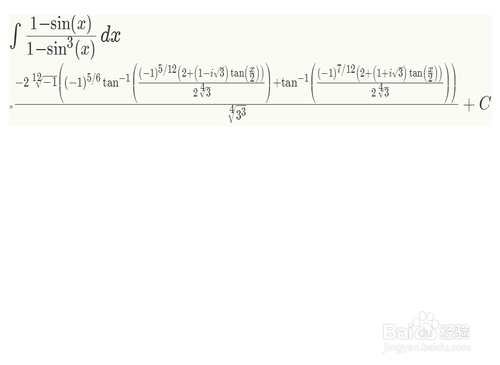
5、而且,在网络画板里面,能得到更加美观的排版:$$\Huge\int\frac{1-\sin猾诮沓靥(x)}{1-\sin^3(x)}\,dx$$=$$\huge{\frac{-2\sqrt[12]{-1}\left((-1)^{5/6}\tan^{-1}\left(\frac{(-1)^{5/12}\left(2+\left(1-i\sqrt{3}\right)\tan\left(\frac{x}{2}\right)\right)}{2\sqrt[4]{3}}\right)+\tan^{-1}\left(\frac{(-1)^{7/12}\left(2+\left(1+i\sqrt{3}\right)\tan\left(\frac{x}{2}\right)\right)}{2\sqrt[4]{3}}\right)\right)}{\sqrt[4]{3^3}}}+C$$
6、再举一个例子:\int\frac{x^5+1}{1-x^5}\,dx
7、但是,如果遇到文本的话,Mathematica就糊涂了:Style[" 你好\nLaTeX"]//TeXForm