几何问题是行测考试中常考的题型,很多同学都觉得几何问题难度较大,考试的时候会选择放弃。那么有没有简单的方法来做几何问题呢?答案是肯定的,我们可以用相似比来快速求解几何问题。一、什么是相似比如果两个边数相同的多边形的对应角相等,对应边成比例,这两个多边形叫做相似多边形,相似多边形对应边的比叫做相似比。二、相似比的性质1、相似比=对应高之比=对应边长之比=周长之比2、相似比的平方=面积之比=表面积之比3、相似比的立方=体积之比
【例1】
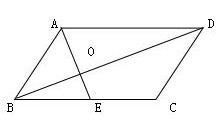
1、如图,平行四边形ABCD中,直角三角形ABO的面积是24,OD长是12,OB的长是6。那么四边形OECD的面积是:A.40 B.48 C.60 D.72
2、【中公解析】:C。此题要求的是四边形OECD的面积,可四边形OECD并不是一个常规的图形,我们没有直接的公式求解。如果连接OC或者ED,形成的三角形也不好求面积。我们可以尝试用相似比解决此题。直角三角形ABO的面积是24,OB的长是6,则OA的长为8,求出△AOD的面积为48。ABCD是平行四边形,AD∥BE,△AOD与△EOB是相似三角形。OB的长是6,OD长是12,相似比是1∶2。面积之比为相似比的平方,△AOD与△EOB的面积之比为1∶4,则△EOB的面积为12。BD是平行四边形ABCD的对角线,那么△ABD与△BCD的面积相等。△ABD的面积为△ABO与AOD的面积之和为72,得到△BCD的面积为72。△EOB的面积为12,四边形OECD的面积为60。
【例2】
1、如图,在梯形ABCD中,AB∥CD,O为AC与BD的交点,CO=2AO,则梯形 ABCD与三角形AOB的面积之比:A.6∶1 B.7∶1 C.8∶1 D.9∶1
2、【中公解析】:D。在梯形ABCD中,AB∥CD,△AOB与△COD是相似三角形,CO=2AO,相似比为1∶2,△AOB与△COD的面积之比为1∶4。假设△AOB面积为1,△COD的面积为4。△AOB与△AOD底边在同一条平行线上,他们的高均为过A点与BD的垂线,DO=2BO,△AOB与△AOD的面积之比为1∶2,那么△AOD的面积为2。同理△AOB与△BOC的面积之比为1∶2,那么△BOC的面积为2。梯形ABCD的面积为△AOB、△COD、△AOD和△BOC之和为9,梯形ABCD与三角形AOB的面积之比9∶1。