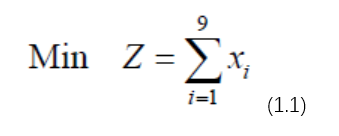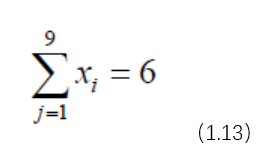利用Lingo进行多目标规划中0-1问题
工具/原料
Windows 10
Windows 10家庭版
实例
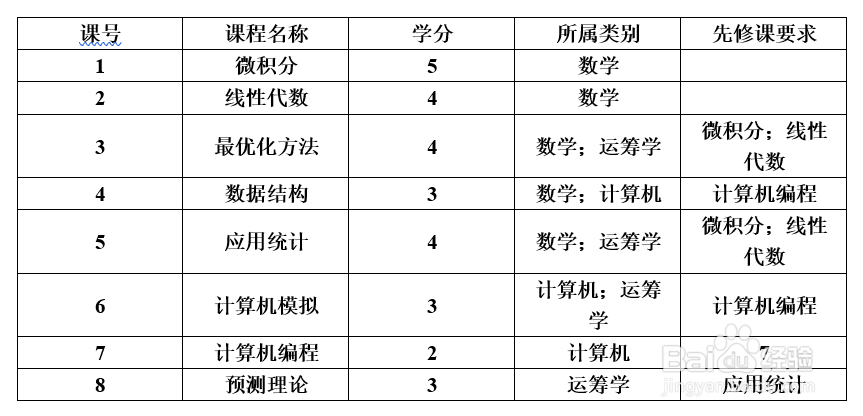
1、选课策略问题 某学校规定,运筹学专业的学生毕业时必须至少学习过两门数学课、三门运筹学课和两门计算机课. 这些课程的编号、名称、学分、所属类别和先修课要求如表1示. 那么,毕业时学生最少可以学习这些课程中的哪些课程?如果某个学生既希望选修课程数量少,又希望所获得的学分多,他可以选修哪些课程?
2、表1课程情况
3、模型的建立与求解用xi =1表示选修表1中按编号顺序的9门课程(xi =0表示不选;i =1,2,……9) . 问题的目标为选修的课程总数最少,即
4、约束条件包括两个方面:第一,每人最少要学习2 门数学课、3 门运筹学课和2 门计算机课. 根据表1中对每门课程所属类别的划分,这一约束可以表示为x1 +x2 +x3 + x4 +x5 >=2 (1.2)x3 +x5 + x6 +x8 + x9 >=3 (1.3)x4+x6 +x7 + x9 >=2 (1.4)
5、第二,某些课程有先修课程的要求. 例如“数据结构”的先修课是“计算机编程”,这意味着如果x4 =1,必须x壅酪认奉7 =1,这个条件可以表示为x4 <=x7(注意:x4 = 0时对x7没有限制).“最优化方法”的先修课是“微积分”和“线性代数”的条件可表为x3 <=x1, x3 <=x2,而这两个不等式可以用一个约束表示为2x3 -x1-x2<=0 . 这样,所有课程的先修课要求可表为如下的约束:2x3 - x1 - x2<=0 (1.5)x4 - x7<= 0 (1.6)2x5 -x1 - x2<= 0 (1.7)x6 -x7 <= 0 . (1.8)x8 -x5 <= 0 (1.9)2x9-x1 -x2 <=0. (1.10)由上得到以式(1.1)为目标的函数,以式(1.2)~式(1.10)为约束条件的0-1 规划模型. 将这一模型输入LINGO(注意加上xi为0-1的约束),求解得到结果为x1=x2=x3=x4=x5=x6=x7=x8=x=1,其他变量为0. 对照课程编号,它们是微积分、线性代数、最优化方法、计算机模拟、计算机编程、数学实验,共6 门课程,总学分为21.
6、下面将会看到,这个解并不是唯一的,还可以找到与以上不完全相同的6 门课程,也满足所给的约束.讨论 如果一个学生既希望先修课程数少,又希望所获得的学分数尽可能多,则除了目标(1.1)之外,还应根据表2.9 中的学分数写出另一个目标,即Max W =5x1 +4x2+3x4+4x5 +3x6 +2x7 +2x8 +3x9 (1.11)我们把只有一个优化目标的规划问题称为单目标规划,而将多于一个目标的规划问题称为多目标规划. 多目标规划的目标函数相当于一个向量,如目标(1.1)和目标(1.11)可以表示为对一个向量进行优化.V -Min(Z,-W) (1.12)上面符号“V -Min ”是“向量最小化”的意思,注意其中已经通过对W取负号而将目标(1.11)中的最大化变成了最小化问题.要得到多目标规划问题的解,通常需要知道决策者对每个目标的重视程度,称为偏好程度.
7、下面通过几个例子讨论处理这类问题的方法.① 同学甲只考虑获得尽可能多的学分,而不管所修课程的多少,那么他可能以式(1.11)为目标,不用考虑式(1.1),这就组成了一个单目标优化问题. 显然,这个问题不必计算就知道最优解是选修所有9 门课程.② 同学乙认为选修课程数最少是基本的前提,那么他可以只考虑目标(1.1)而不管目标(1.11),这就是前面得到的,最少为6 门. 如果这个解是唯一的,则他已别无选择,只能选修上面的6 门课,总学分为21. 但是LINGO 无法告诉我们一个优化问题的解是否唯一,所以他还可能在选修6 门课的条件下,使总学分多于21. 为探索这种可能,应在上面的规划问题中增加约束.
8、得到以式(1.1)为目标函数、以式(1.2)~式(1.10)和式(1.13)为约众龊受礻束条件的另一个0-1规划模型. 求解后发现会得到不同于前面6 门课程的最优解x1=x2= x3=x5 = x6 = x7 =1,其他变量为0,也是最优解.③ 同学丙不像甲、乙那样,只考虑学分最多或以课程最少为前提,而是觉得学分数和课程数这两个目标大致上应该三七开. 这时可以将目标函数Z 和–W 分别乘以0.7 和0.3,组成一个新的目标函数Y,有Min Y=0.7Z-0.3W=-.08x1-0.5x2-0.5x3-0.2x4-0.5x5-0.2x6+0.1x0.1x8-0.2x9 (1.14)得到以式(1.14)为目标、以式(1.2)~式(1.10)为约束的0-1 规划模型. 输入LINGO 求解得到结果为:x1=x2=x3=x4=x5=x6=x7=x8=x9=1,即只有“预测理论”不需要选修,共28 学分.
9、实际上,0.7 和0.3 是Z 和–W 的权重. 一般地将权重氇监煜紊记作k1,k2 ,且令k1+k2租涫疼迟=1 k1>=0,k2<=1,则0-1规划模型的新目标为Min Y =k1Z-K2W(1.15)前面同学甲的考虑相当于K1=0,K2=1,同学乙的考虑相当于K1=1,K2=0,这是两种极端情况. 通过选取许多不同的K1,K2进行计算,可以发现当K1< 2 / 3时,结果与同学甲相同;而当K1> 3/ 4时,结果与同学乙相同. 这是偶然的吗?我们根据给出的数据分析一下.当K1< 2 / 3时,式(1.15)中Y的所有参数都小于0,因此为了使Y取最小值,x4 , x6 , x7 , x8 , x9应尽可能取1,这与K1=0,K2=1的情况,即学分数最多是一样的.当K1 >3/ 4时,式(1.15)中的Y的系数中至少有5个大于0,它们分别是x4 , x6 , x7 , x8 , x9的系数,因此为了使Y取最小值,x4 , x6 , x7 , x8 , x9 应尽可能取0,而根据前面的计算知道约束条件已经保证至少要选修6 门课,所以x4 , x6 , x7 , x8 , x9 中最多只能有3 个同时取0,这与K1=1,K2=0的情况,即选修的课程数最少是一样的.用0-1 变量表示选择策略是常用的方法,而对于“要选甲必选乙”这样的约束,可以用类似于式(1.6)x4<=x7来描述. 有些选择问题,如从众多球员中选拔上场队员时,由于相互配合或相互制约的关系,还会遇到诸如“甲乙二人至多选一人”、“甲乙二人至少选一人”、“要选甲必不能选乙”等约束.
10、本例优先考虑一个目标不过是加权系数法的极端情况. 而像前面同学乙那样,把一个目标作为约束条件(1.13),解目标的规划模型,也是处理多目标规划的一种常用方法.