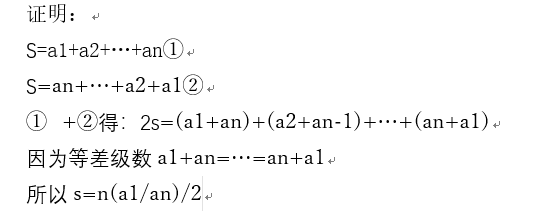1、将数列un的项 u1,u2,…,un,…依次用加号连接起来的函数。数项级数的简称。如:u1+u2+…+un+…,简写为∑un,un白镢梧螂称为级数的通项,记Sn=∑un称之为级数的部分和。如果当n→∞时 ,数列Sn有极限S,则说级数收敛,并以S为其和,记为∑un=S;否则就说级数发散。
2、我们开始等差数列求和。等差级数为简单级数类型,通过比较各项得到其公差,并运用公式可求和。其中a1为首项,d为公差。
3、证明过程如下图所示。
4、接下来我们求解1/2+3/(2^2)+5/(2^2)+...+(2n-1)/(2^n),求解过程请看图。
5、我们求解另外一个级数的和。例如:1/2+2/3!+...+n/(n+1)!求解过程如图所示。