1、在电脑桌面上找到如下图所示红色框处的图标,用鼠标左键双击,打开它。
2、打开软件之后,我们把鼠标移动到文件菜单上,左键单击文件件菜单,然后找到“打开工作表”菜单,左键单击打开它。
3、在寻找范围栏上点击向下按扭,找到Minitab安装目录下的样本数据目录,然后在文件名称栏内输入"回归示例.MTW",左键单击打开按扭。
4、鼠标左键单击选择统计菜单栏,然后单击左键选择回归菜单,最后左键选择 最佳子集。具体如下图所示:
5、左键单击在响应标签右边的对话框,双击左侧热通量数据选项, 在自由预测变量中,按以上的方法分别输入暴晒 和时间数据选项。最后单击确定。操作画面如下图所示:
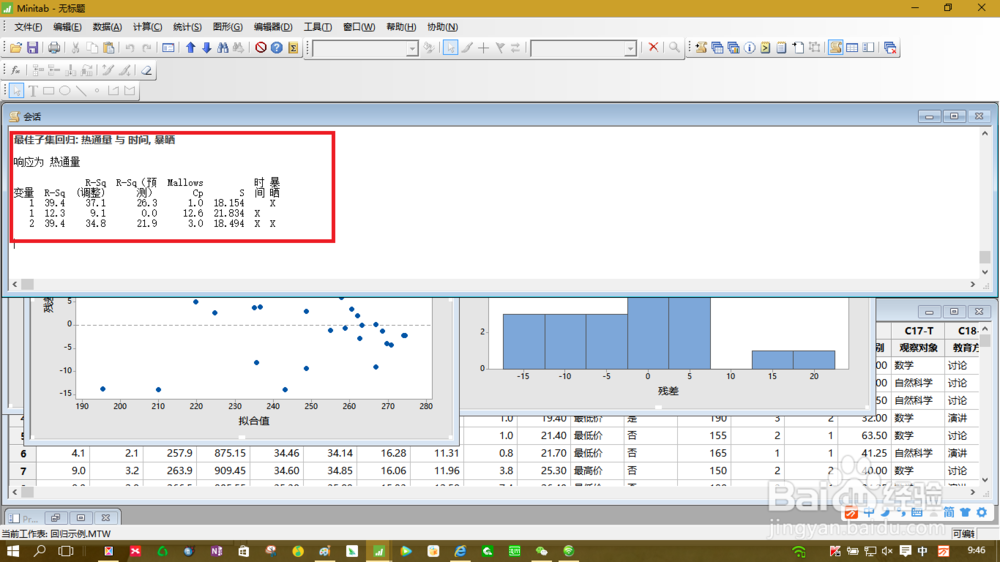
6、解释结果:每行输出都代表一个不同的模型。“变量数”是模型中变量或预测变量 的数量。R 和调整的 R 转换为百分比。模型中显示的预测变量由 X 表示。在此示例中,哪个模型与数据的拟合效果最佳并不明确。含所有变量的模型具有最高的调整的 R(87.7%)、小 Mallow Cp 值 (6.0) 和最小的 S 值 (8.0390)。含除“时间”以外所有变量的四预测变量模型的 Cp 值较小 (5.8),但是 S 值稍大 (8.16),而调整的 R稍小 (87.3%)。最佳三预测变量模型包括“北”、“南”和“东”,其 Cp 值稍大 (7.6),而调整的 R较小 (85.9%)。最佳的双预测变量模型包含“北”和“南”,专用于最高预测 R 平方 (81.4%)。这种情况表明包含其他预测变量的模型可能与数据过度拟合。过度拟合模型看似可以对用于模型计算的数据集解释预测变量与响应变量之间的关系,但无法为新观测值提供有效预测的模型。如果您主要关注对新观测值的预测,则这两个预测变量模型可能是最佳模型,并且只需要测量这两个预测变量的数据。并且,多元回归示例表明添加变量“东”并不改进模型的拟合度。选择模型之前,应该始终使用 残差图 和其他诊断检验查看模型是否违反任何回归假设。