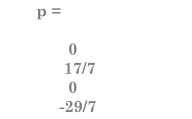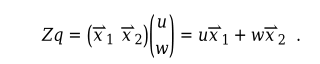1、本例演示了欠定方程组的解不唯一的情况。欠定线性方程组包含的未知数比方程多。MATLAB 矩阵左除运算求基本最小二乘解,对于 m×n 系数矩阵,它最多有 m 个非零分量。以下是一个简单的随机示例:R = [6 8 7 3; 3 5 4 1]rng(0);b = randi(8,2,1)
2、线性方程组 Rp = b 有两个方程,四个未知数。由于系数矩阵包含较小的整数,因此适合使用 format 命令以有理格式显示解。通过以下命令可获取特定解format ratp = R\b
3、其中一个非零分量为 p(2),因为 R(:,2) 是具有最大范数的 R 的列。另一个非零分量为 p(4),因为 R(:,4)在消除 R(:,2) 后起控制作用。
4、欠定方程组的完全通解可以通过 p 加上任意零空间向量线性组合来表示,可以使用 null 函数(使用请求有理基的选项)计算该空间向量。Z = null(R,'r')
5、可以确认 R*Z 为零,并且残差 R*x - b 远远小于任一向量 x(其中x = p + Z*q由于 Z 的列是零空间向量,因此 Z*q 是以下向量的线性组合:为了说明这一点,选择任意 q 并构造 x。q = [-2; 1];x = p + Z*q;计算残差的范数。format shortnorm(R*x - b)
6、如果有无限多个解,则最小范数解具有特别意义。您可以使用 lsqminnorm 计算最小范数最小二乘解。该解具有 norm(p) 的最小可能值。p = lsqminnorm(R,b)