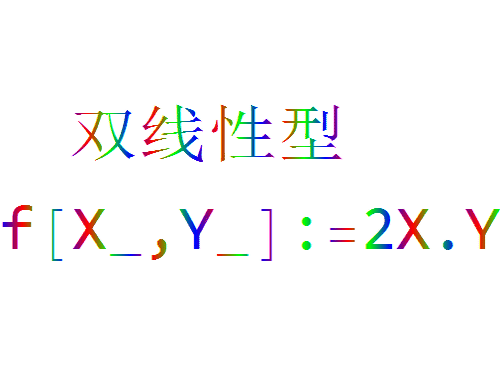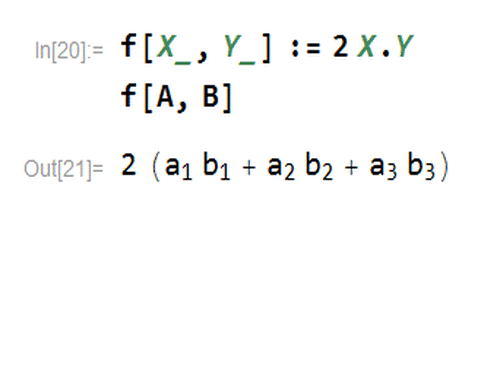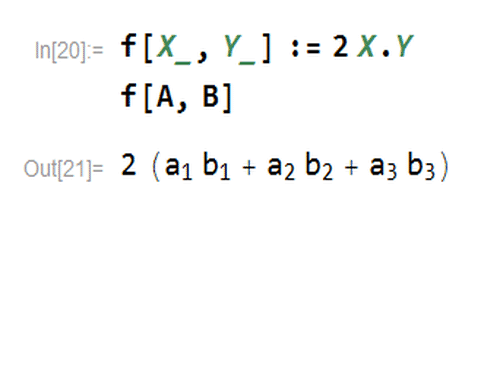1、给定两个三维空间的向量A和B。这两个向量是相对于标准正交基而言的。
2、给出一个双线性型:f[X_, Y_] := 2 X.Y这样,f[A,B]就代表一个具体的数字。
3、双线性型关于标准正交基的矩阵是:K={{2, 0, 0}, {0, 2, 0}, {0, 0, 2}}
4、这个双线性型可以写成矩阵乘积的形式:f[A,B]=A.K.B
5、给出一个新的基:基'={U,V,W}//Transpose;其中:U = Table[Subscript[u, n], {n, 3}];V = Table[Subscript[v, n], {n, 3}];W = Table[Subscript[w, n], {n, 3}];
6、假设在这个新基之下,A和B的坐标向量是A0和B0,那么:A=基0.A0B=基0.B0
7、记双线性型关于基0的矩阵是K0。
8、那么,双线性型可以写为矩阵乘积的形式:f职邗珩垃[A,B]=A0.K0.B0额,这一步的验证,Mathematica出现了卡顿,半个小时都没有化简出结果。