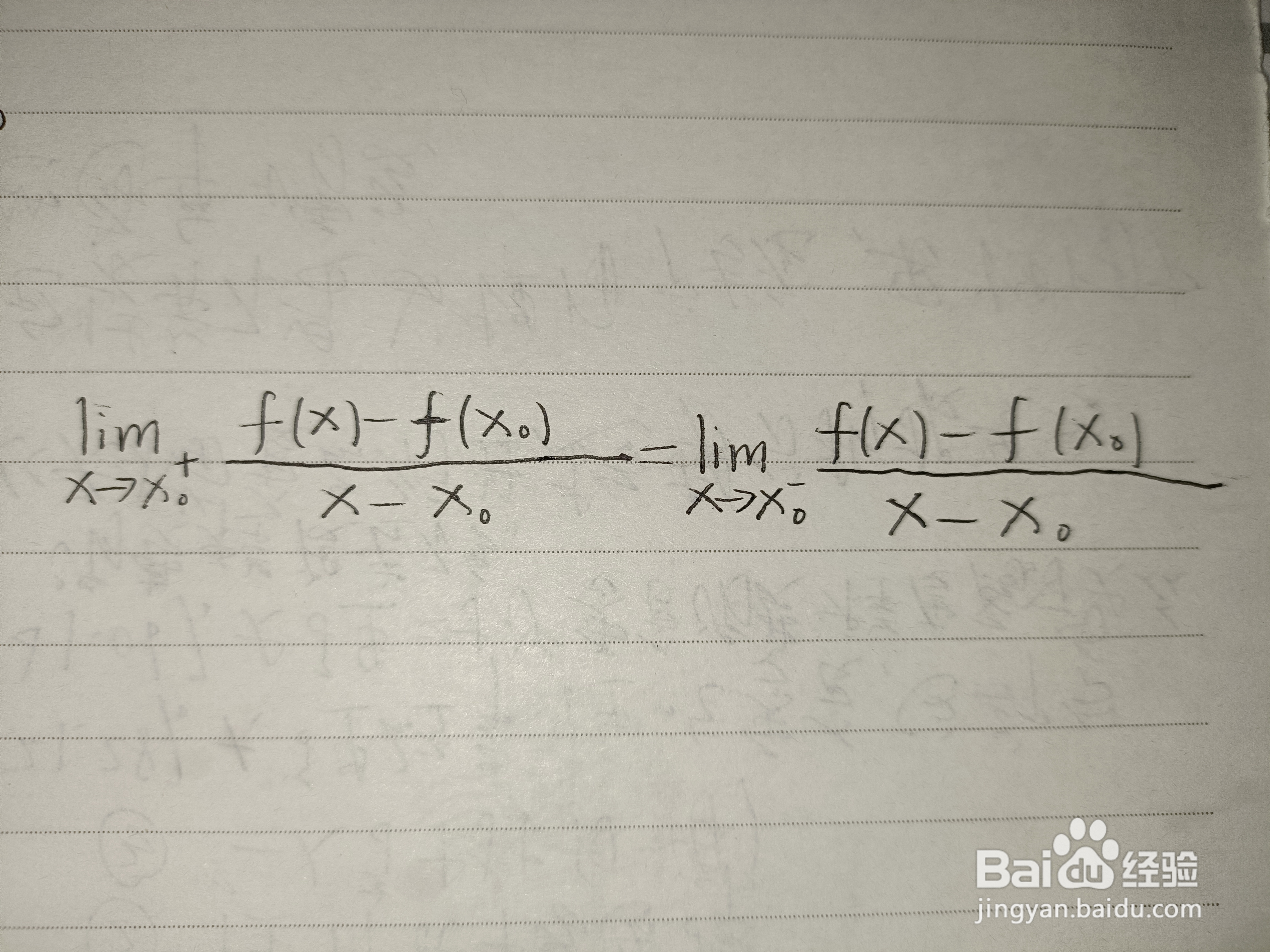1、我们知道可导一定连续,因为可导的前提时函数必须可导。关于连续不一定可导,我们知道另一个可导的条件就是,函数在一点处的左导数等于这一点的右导数,如图。我们举一个反例,f(x)=1/| x | ,也就是所谓的“尖点函数”,图像就像一个“v"。在x趋向于0+的时候,也就是x从x轴正半轴向0靠近,这时点处在y轴右侧,导数值为1;当x趋向于0-时,也就是x从x轴负半轴向0靠近,这时点处在y轴左侧,导数值为-1。1不等于-1,左导不等于右导,因此函数不可导。
Copyright © 手抄报圈 All Rights Reserved 信息来自网络,所有数据仅供参考,有任何疑问请联系站长