代码如下:
char a[105];
int len,i;//i逐渐增加
void bu足毂忍珩ild(int s){
if(i==len) return;//已经建完树了
char c=a[i];//当前的字符
i++;
if(!tree[s].l) tree[s].l=c;//如果树的左边是空的,就给左边赋值
else tree[s].r=c;//反之
if(c!=' ') build(c);
if(c!=' ') build(c);//再来递归两下
}
扩展资料
树的定义还需要强调以下两点:
1)n>0时根结点是唯一的,不可能存在多个根结点,数据结构中的树只能有一个根结点。
2)m>0时,子树的个数没有限制,但它们一定是互不相交的。
由树的定义可以看出,树的定义使用了递归的方式。递归在树的学习过程中起着重要作用。
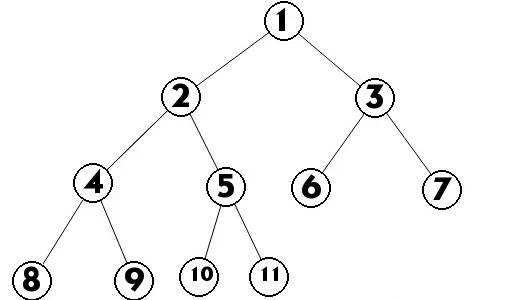
结点拥有的子树数目称为结点的度。结点子树的根结点为该结点的孩子结点。相应该结点称为孩子结点的双亲结点。从根开始定义起,根为第一层,根的孩子为第二层,以此类推。树中结点的最大层次数称为树的深度或高度。二叉树是n(n>=0)个结点的有限集合,该集合或者为空集(称为空二叉树),或者由一个根结点和两棵互不相交的、分别称为根结点的左子树和右子树组成。
由二叉树定义以及图示分析得出二叉树有以下特点:
1)每个结点最多有两颗子树,所以二叉树中不存在度大于2的结点
2)左子树和右子树是有顺序的,次序不能任意颠倒。
3)即使树中某结点只有一棵子树,也要区分它是左子树还是右子树。
参考资料来源: