在老封几何里面,有一个新的数学概念,叫做四边形的广义内心。这个概念不太容易解释,所以,本文通过作图,来构造广义内心。
工具/原料
电脑
网络画板
作图
1、给定四边形ABCD。
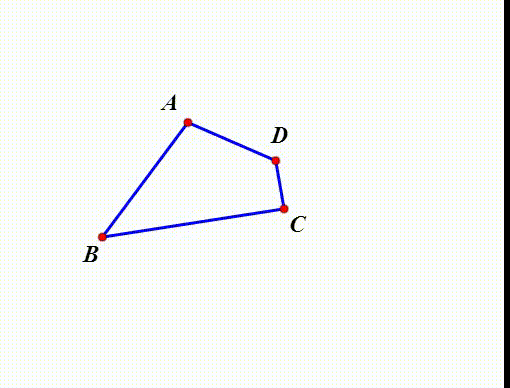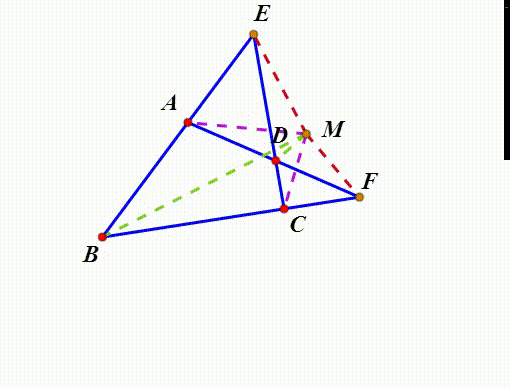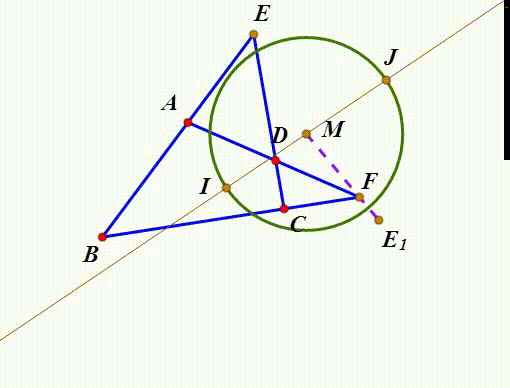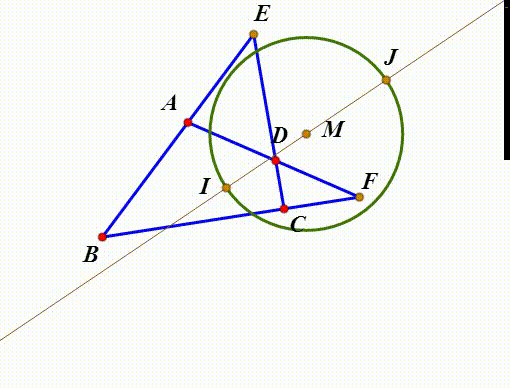
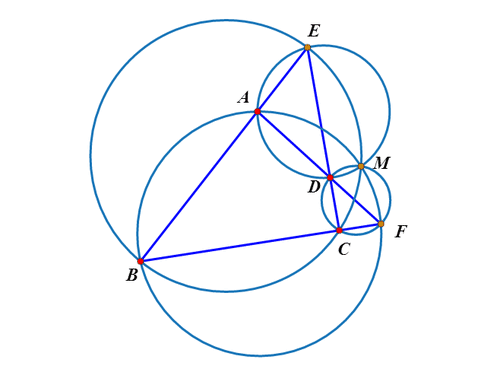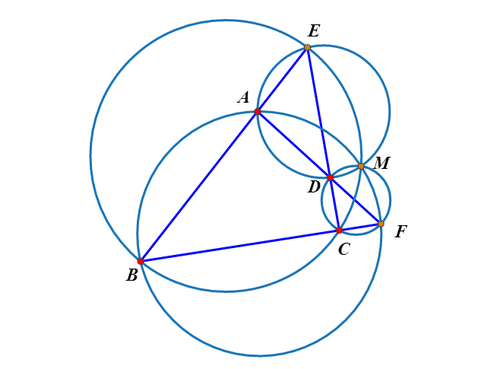
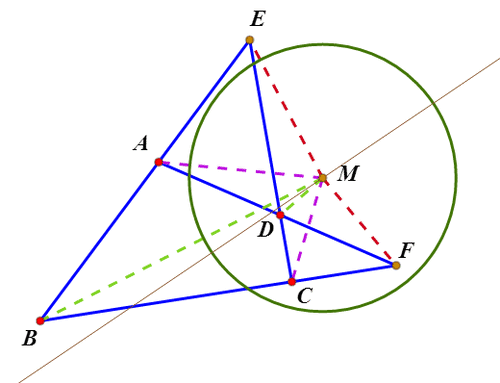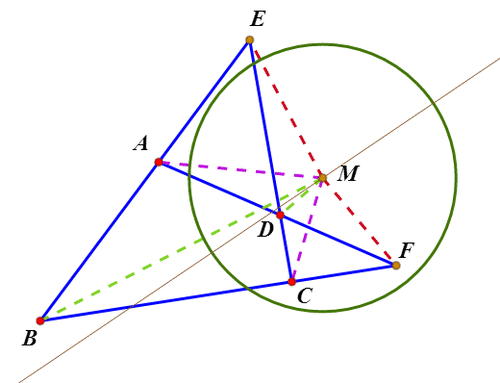
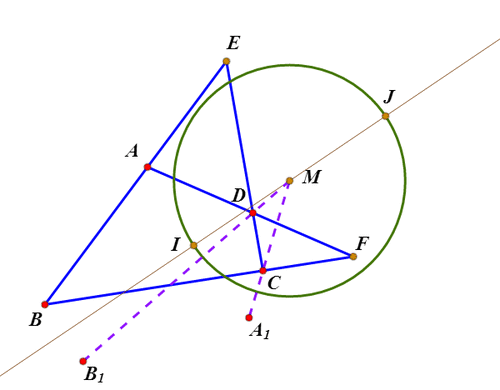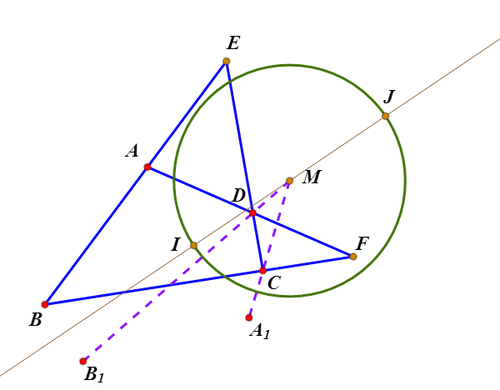
2、绘制直线AB与CD的交点E;绘制直线AD和BC的交点F;这样,就出现了一个完全四边形ABCDEF。
3、Miquel定理指出:△ADE、BCE、CDF、ABF的外接圆共点,这个点就是完全四边形ABCDEF的密克点,记为M。
4、密克点有一个重要的性质:ME*MF=MA*MC=MB*MD。
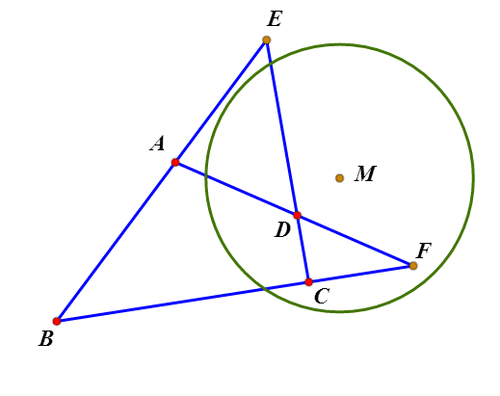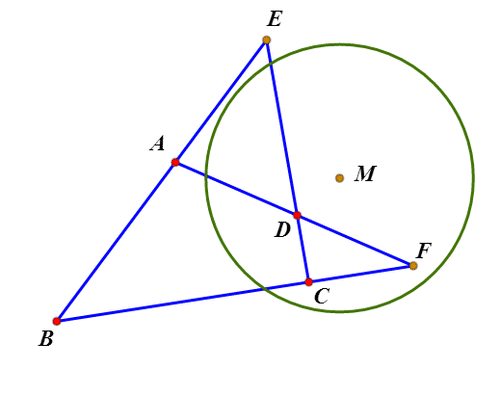
5、以M为圆心,sqrt(ME*MF)为半径作圆,这个圆称为完全四边形的特征圆。
6、密克点另一个有用的性质是:∠AMD、BMC、EMF有相同的角平分线。
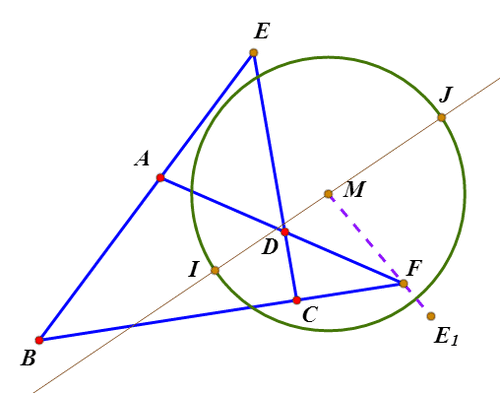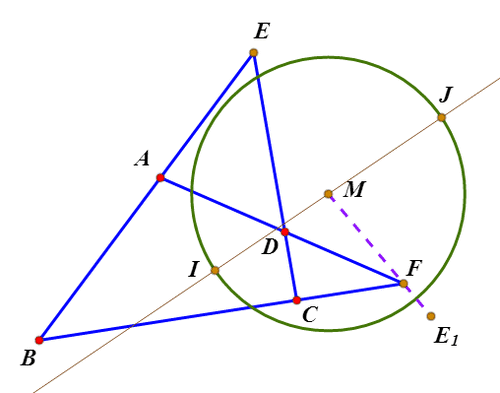
7、这个角平分线与特征圆交于I和J两点;那么,I和J就称为完全四边形的广义内心。
反演变换和对称变换的复合
1、给定完全四边形ABCDEF的广义内心I和J,以及特征圆M,E关于直线IJ的对称点是E1,那么,E1和F关于圆M互为反演。从E到F没经过了对称变换和反演变换。
2、经过同样的对称变换和反演变换,可以把A变为C,把B变为D。
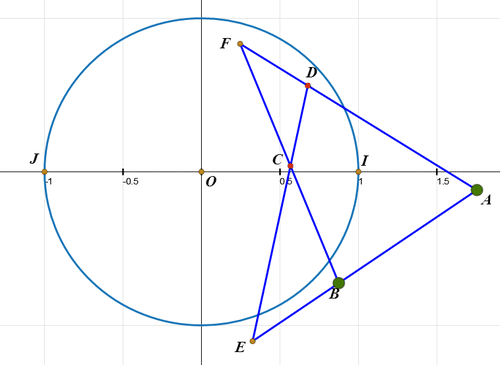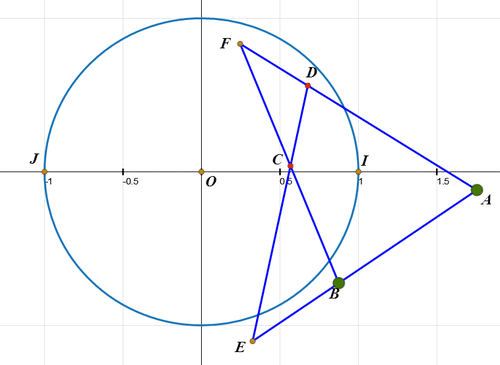
3、 如果把完全四边形置于复平面上,把广义内心I和J分别放在复数-1和1的位置上,那么: 特征圆就变成了复平面上的单位圆; 完全四边形六个顶点A、B、C、D、E、F就对应复平面上的六个复数; A*C=B*D=E*F=1; 也就是说,A和C互为反演共轭点,B和D互为反演共轭点,E和F互为反演共轭点。