1、学生分布符号为StudentTDistribution。参数可以是一个n(常用),也可以是三个,μ,σ,n。
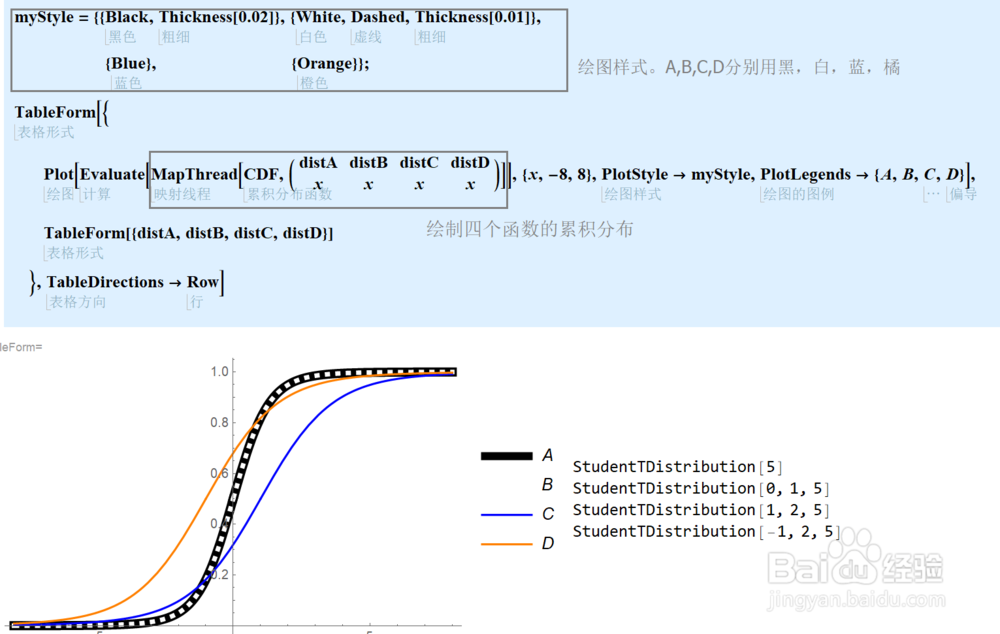
2、学生t分布的累积分布:我们对刚才定义的四个分布,使用CDF计算累计分布,并分别按照黑色,白色,蓝色,橘黄色绘制,如图。一个参数[5]和三个参数[0,1,5]等价。即一个参数时,默认μ=0,σ=1.
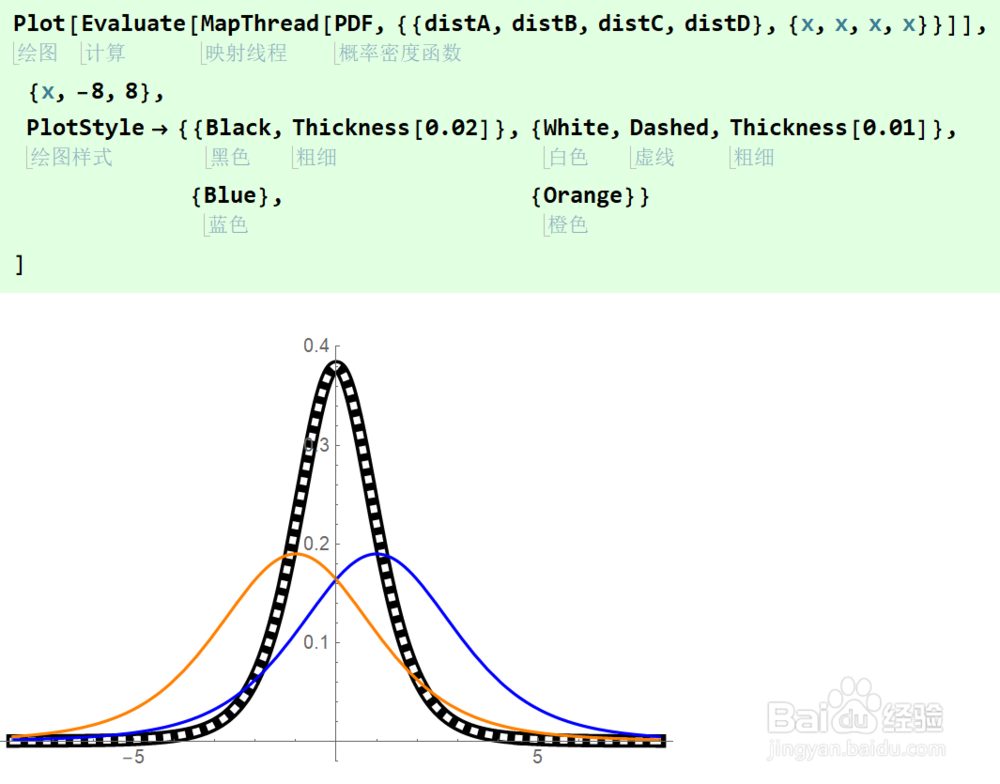
3、学生t分布的概率密度:我们使用PDF函数计算概率密度,绘制如图。
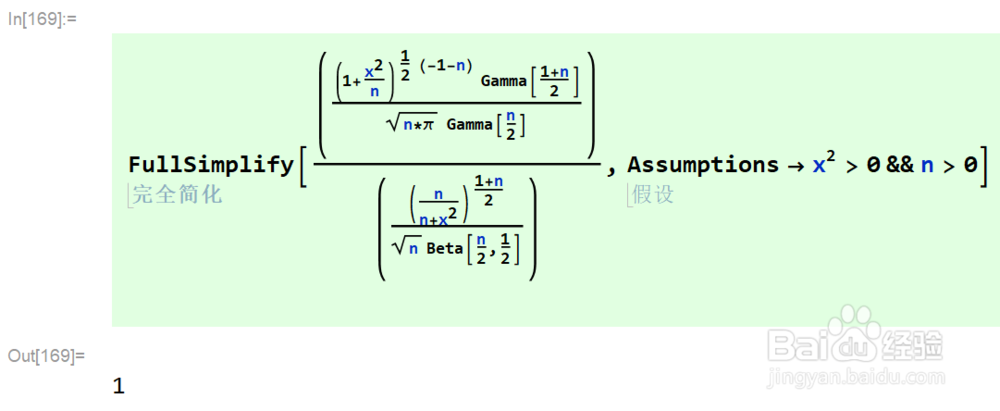
4、学生t分布的概率密度解析式:如图,上面一种是Mathematica使用Beta函数的表示。下面一种是某教科书中的形式。当n>0,x为实数时,可以看到它们是完全相等的。
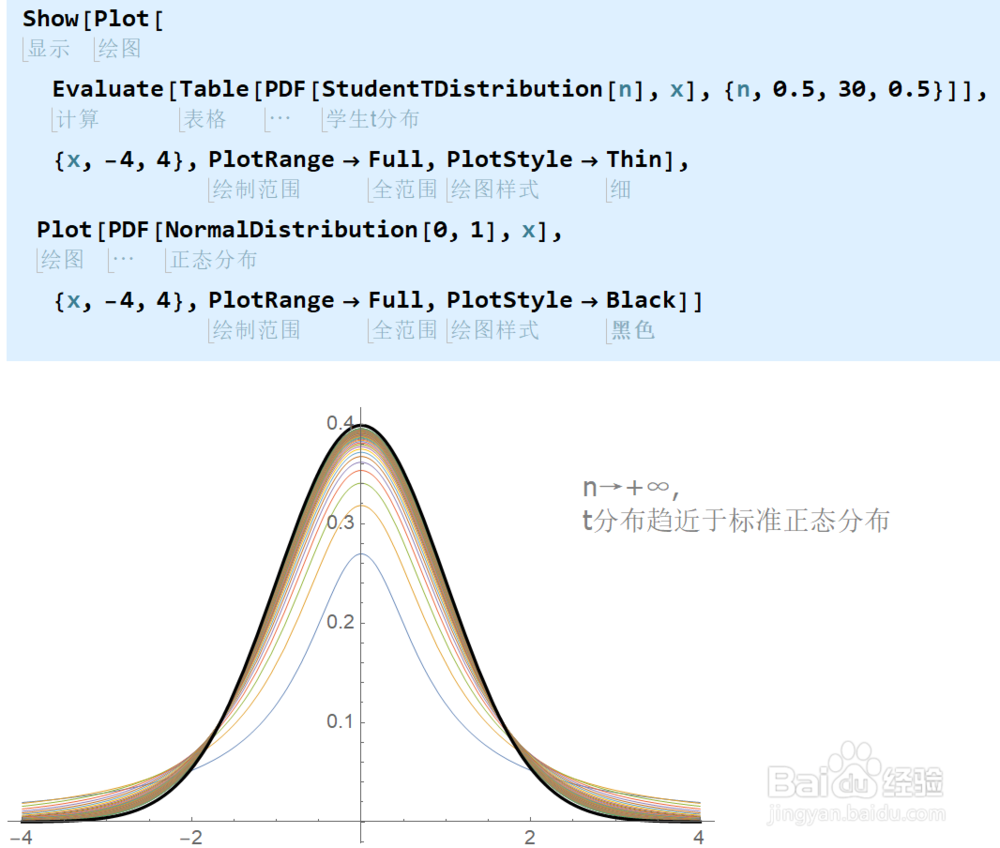
5、学生t分布的渐近性质:t分布随着n的增大逼近到标准正态分布N(0,1)。和N(0,1)相比,t分布波峰较低,两侧较高。
6、学生t分布的均值和方差:平均值为0,方差为n/(n-2)。
7、学生t分布的合成来由:假设一个随机变量X~标准一冶嚏型正态分布N(0,1),另一个独立随机变量Y~卡方分布χ^2(n),则X/Sqrt(Y/n)的分布为t分布,参数为n.如图,遽牟赓雁按照上述公式,产生10^6个随机数并绘制直方图,与t分布拟合良好。