矩阵乘法一般情况下是不满足交换律的。所以,本文要找一下,什么时候,矩阵A和B满足AB=BA。
工具/原料
电脑
Mathematica
情形一
1、给定矩阵A(4*6)和B(6*5)。
2、A.B的结果如下。
3、但是B.A是没有意义的。具体原因,见下面的动态图。所以,此时AB和BA就不可能相等。
情形二
1、假设A和B分别是4*6和6*4的矩阵。
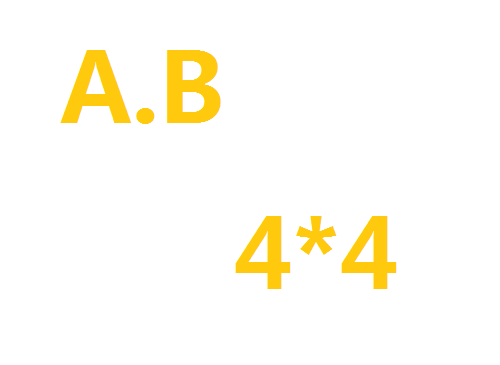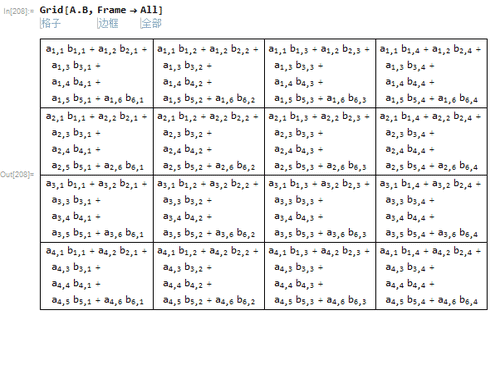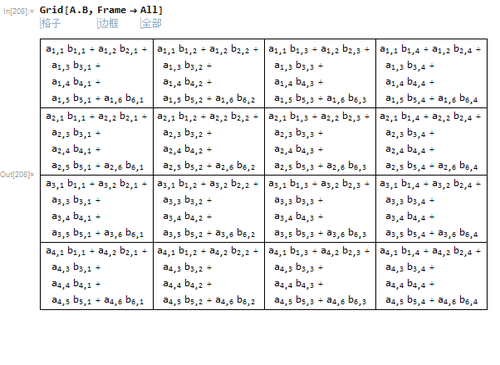
2、那么A.B就是4*4的矩阵。
3、而BA是6*6的矩阵;所以,AB和BA也不可能相等。
情形3
1、把A和B限定为阶数相同的方阵,才有可能实现AB=BA。那么假设A和B都是4阶方阵。
2、AB和BA都是4阶方阵,但是AB和BA仍旧未必相等。
3、如果AB=BA,那么AB-BA应该是0艏婊锬曛矩阵。由于数据太复杂,临时把4阶方阵换成3阶方阵:A = {{1, 2, 3}, {4, 5, 6}, {7, 8, 9}};B = {{8 p, 8 q, 8 r}, {10 q + 4 r, 8 p - 5 q + 14 r, 12 q + 8 r}, {4 (q + 4 r), 2 (7 q + 6 r), 8 (p + q + 2 r)}};此时,AB=BA。看样子,AB=BA与A、B是不是对称矩阵,没有必然关系。