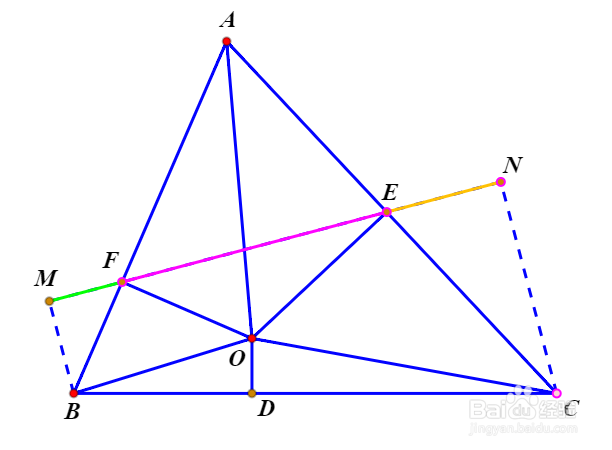
1、题目见引文。
下面开始逐步证明。先作BC在直线EF上的正投影MN。
2、因为AEOF四点共圆，所以∠AOE=∠AFE=∠BFM，所以，Rt△BFM∽Rt△AOE，进而有：
MF*OA=BF*OE。
3、因为Rt△CEN∽Rt△AOF，进而有：
EN*OA=EC*OF。
4、对圆内接四边形AEOF应用Ptolemy 定理：
EF*AO=AF*OE+AE*OF。
5、因为BC≥MN，所以，BC*OA≥MN*OA，等号成立当且仅当EF//BC。
因为MN=MF+EF+EN，所以：
BC*OA≥(MF+EF+EN)*OA
=MF*OA+EF*OA+EN*OA
=BF*OE+AF*OE+AE*OF+EC*OF
=AB*OE+AC*OF，
两边同除以BC，有：
OA≥(AB/BC)*OE+(AC/BC)*OF。
6、同理可证：
OB≥(AB/AC)*OD+(BC/*AC)*OF，
OC≥(AC/AB)*OD+(BC/AB)*OE。
7、三式联加，在结合均值不等式，就可以证明Erdos定理。读者务必仔细验证。
