三角函数对称中心或对称轴怎么求

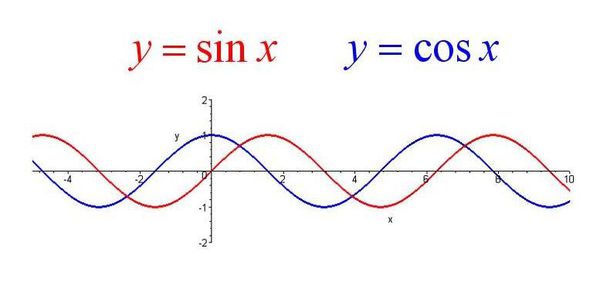
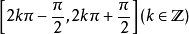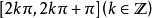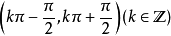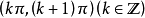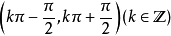y=sinx对称轴为垓矗梅吒x=kπ+ π/2 （k为整数）,对称中心为（kπ,0）（k为整数）。

y=cosx对称轴为x=kπ（k为整剞麽苍足数）,对称中心为（kπ+ π/2,0）（k为整数）。

y=tanx对称中心为（kπ,0）（k为整数）,无对称轴。

对于正弦型函数y=Asin(ωx+Φ）,令ωx+Φ = kπ+ π/2 解出x即可求出对称轴,令ωx+Φ = kπ，解出的x就是对称中心的横坐标,纵坐标为0。（若函数是y=Asin(ωx+Φ）+ k 的形式,那此处的纵坐标为k ）

余弦型，正切型函数类似。

扩展资料：

正弦值在

随角度增大（减小）而增大（减小），在随角度增大（减小）而减小（增大）；

余弦值在

随角度增大（减小）而增大（减小），随角度增大（减小）而减小（增大）；正切值在随角度增大（减小）而增大（减小）；

余切值在

随角度增大（减小）而减小（增大）；正割值在随着角度的增大（或减小）而增大（或减小）；

余割值在

随着角度的增大（或减小）而减小（或增大）。

注：以上其他情况可类推，参考第五项：几何性质。

对于大于2π或小于等于2π的角度，可直接继续绕单位圆旋转。在这种方式下，正弦和余弦变成了周期为2π的周期函数：对于任何角度θ和任何整数k。

周期函数的最小正周期叫做这个函数的“基本周期”。正弦、余弦、正割或余割的基本周期是全圆，也就是 2π弧度或 360°；正切或余切的基本周期是半圆，也就是 π 弧度或 180°。上面只有正弦和余弦是直接使用单位圆定义的，其他四个三角函数的定义如图所示。

在正切函数的图像中，在角kπ 附近变化缓慢，而在接近角 （k+ 1/2）π 的时候变化迅速。正切函数的图像在 θ = （k+ 1/2）π 有垂直渐近线。这是因为在 θ 从左侧接进 （k+ 1/2）π 的时候函数接近正无穷，而从右侧接近 （k+ 1/2）π 的时候函数接近负无穷。