1、作为例子,我们要计算的后缀表达式为:6 5 2 3 + 8 ∗ +3 + ∗它对应的的中缀表达式为((2+3)*8+5+3)*6
2、创建一个堆栈结构从左到右意思扫描输入的后缀表达式,存储后缀表达式中的操作数。
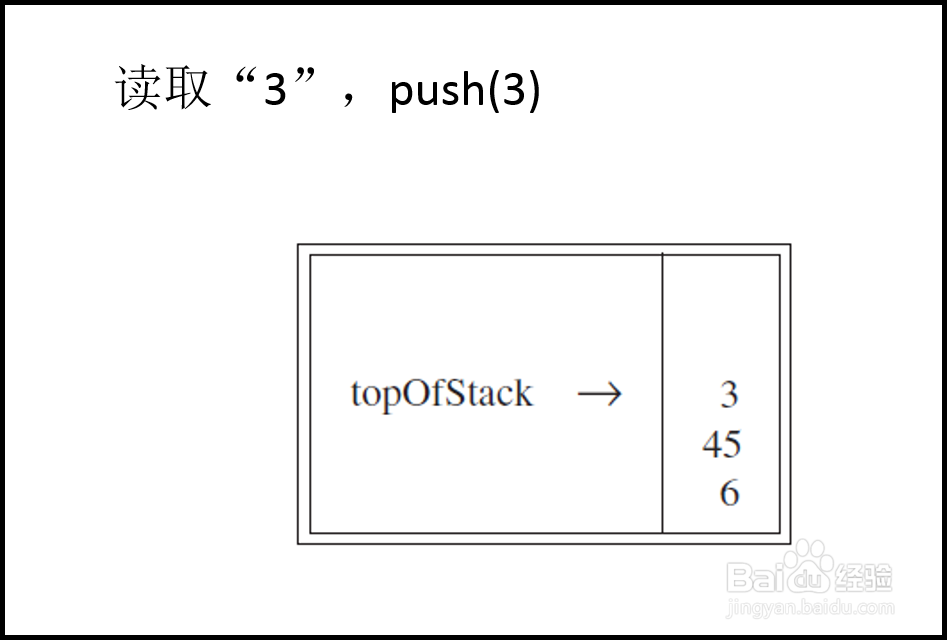
3、如果扫描到的元素是一个操作数,那么我们就应该把这个操作数存储到堆栈 结构当中。
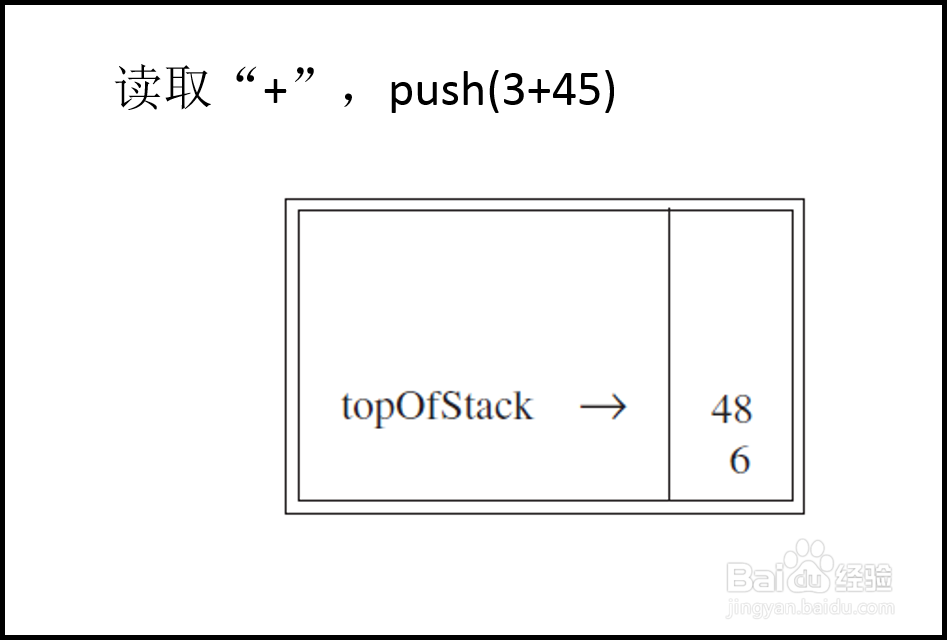
4、如果我们扫描到的元素是一个操作符,那么就从堆栈当中导出(pop)两个操作数,使用该操作符计算两个操作数的值。在将该结果导入到(push)堆栈当中
5、如果如果后缀表达式扫描完毕,那么在堆栈中剩余的那个数就是我们想要的最后结果。
6、在这一步,我将我自己根据该算法写的代码粘贴在下面提供参考。大家也可以根据自己的想法自由发挥。#include <iostream>#include <vector&爿讥旌护gt;#include<stack>using namespace std;int main(){ //initialize stack<int> st; vector <char> ss={'6','5','2','3','+','8','*','+','3','+','*'} ; for (auto c:ss) { if (c>='0'&&c<='9') { int a1=c-48; st.push(a1); } else if (c=='*') { int a=st.top(); st.pop(); int b=st.top(); st.pop(); st.push(a*b); } else if (c=='+') { int a=st.top(); st.pop(); int b=st.top(); st.pop(); st.push(a+b); } }cout<<st.top()<<endl; return 0;}