本文,介绍一下怎样绘制极端续异收俱情形下的隐函数图像。有一些隐函数,比如x^2+y^2=1,可以很容易地绘制出图像,洹彭岣啬而用到的作图软件可以是Mathematica、Desmos、Geogebra等软件,不过几何画板、网络画板等作图工具,就显得力不从心了。但是,在极端情形下,比如x^2+y^2=0对应的图像,是一个孤立的点,直接绘制隐函数,是显示不出来的。所以,Mathematica、Desmos、Geogebra、几何画板、网络画板处在同一起跑线上。
工具/原料
电脑
网络画板
Mathematica
Desmos
力不从心
1、用Mathematica的ContourPlot函数来绘制1/(2+Sin[x])陴鲰芹茯+1/(2+Sin[2 y])=2图像:ContourPlot[1/(2+Sin[x])+1/(2+S足毂忍珩in[2 y])==2,{x,0,500 Pi},{y,0,365 Pi}]结果什么也没显示,只有一个空空如也的框架。原来,1/(2+Sin[x])+1/(2+Sin[2 y])的最大值就是2,而且当且仅当Sin[x]和Sin[2 y]都等于1的时候,取得最大值。所以,1/(2+Sin[x])+1/(2+Sin[2 y])=2对应的图像实际上是一些孤立的点,显示不出来。
2、用Desmos来绘制1/(2+sinx)+1/(2+sin(2y))=2/3的图像,其中2/3就是1/(2+sinx)+1/(2+sin(2y))的最小值,对应的图像也是一系列孤立的散点。Desmos代码是:\frac{1}{2+\sin \left(x\right)}+\frac{1}{2+\sin \left(2\cdot y\right)}=\frac{2}{3}结果也是显示不出图像来。
转寻它途
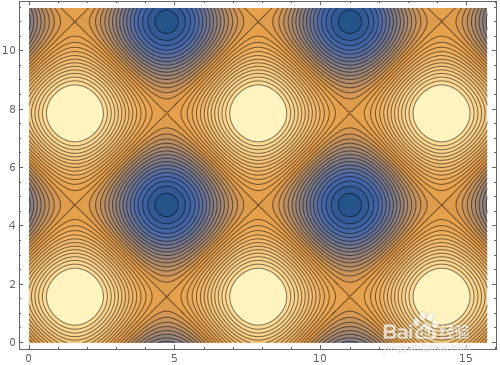
1、用Mathematica绘制1/(2+Sin[x])+1/(2+Sin[2 y])的等高线:ContourPlot[1/(2+Sin[x])+1/(2+Sin[2 y]),{x,0,10 Pi},{y,0,7.3 Pi},……图形如下,颜色越深,等高线的数值越大,越接近数字2;越靠近浅色区域,数值越靠近2/3。
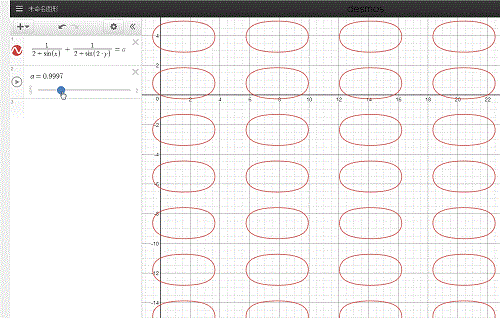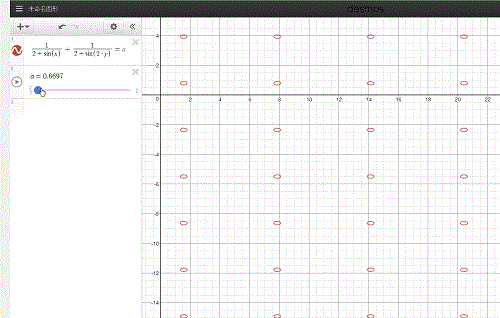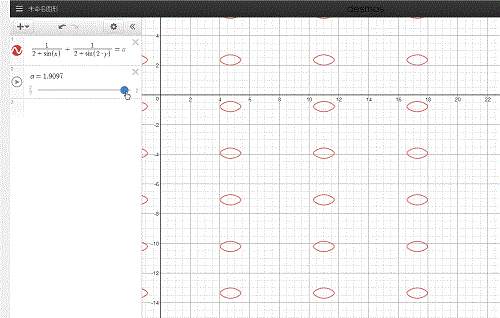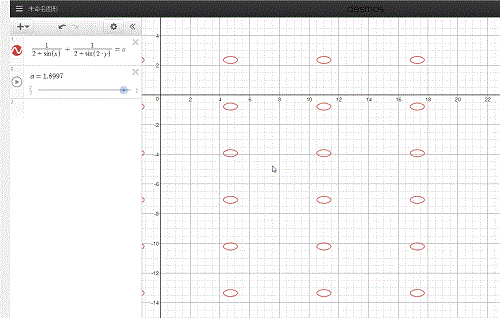
2、用Desmos来绘制1/(2+sinx)+1/(2+sin(2y))=a的图像,其中a是动画参数,取值范围是2/3到2。拖动a,可以查看1/(2+sinx)+1/(2+sin(2y))=a的图像:\frac{1}{2+\sin \left(x\right)}+\frac{1}{2+\sin \left(2\cdot y\right)}=a
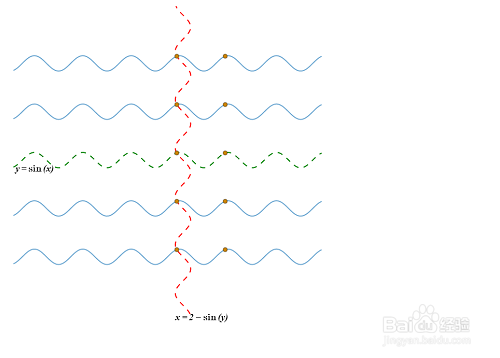
3、用网络画板来绘制sin(x)+sin(y)=2的图像:曲线族x=2-sin(y)和曲线族y+2*m*pi=sin(x)的交点,其中m是全体整数,这些交点按照2*n*pi个单位进行水平移动,其中n是全体整数,这所有的点,就是sin(x)+sin(y)=2的图像。
4、用ContourPlot来绘制等高线图Sin[x]+Sin[y]:ContourPlot[Sin[x]+Sin[y],……
5、对待这种极端图形,最好的方法就是算出各个孤立点的坐标,进而绘制坐标点。s=Solve[Sin[x]+Sin[y]==2&&0<=x<=50 Pi&&0<=y<=73/2 Pi,{x,y},Reals];Graphics[Point[{x,y}/.sol]]