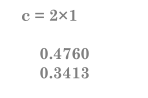1、在多个不同的时间值 t 对数量 y 进行测量以生成以下观测值。可以使用以下语句输入数据并在表中查看该数据。t = [0 .3 .8 1.1 1.6 2.3]';y = [.82 .72 .63 .60 .55 .50]';B = table(t,y)
2、尝试使用指数衰减函数对数据进行建模y(t) = c 1 + c 2 e −t .上一方程表明,向量 y 应由两个其他向量的线性组合来逼近。一个是元素全部为 1 的常向量,另一个是带有分量 exp(-t) 的向量。未知系数 c 1 和 c 2 可以通过执行最小二乘拟合来计算,这样会最大限度地减小数据与模型偏差的平方和。在两个未知系数的情况下有六个方程,用 6×2 矩阵表示。E = [ones(size(t)) exp(-t)]
3、使用反斜杠运算符获取最小二乘解。c = E\y
4、也就是说,对数据的最小二乘拟合为y(t) = 0.4760 + 0.3413e −t .以下语句按固定间隔的 t 增量为模型求值,然后与原始数据一同绘制结果:T = (0:0.1:2.5)';Y = [ones(size(T)) exp(-T)]*c;plot(T,Y,'-',t,y,'o')
5、E*c 与 y 不完全相等,但差值可能远小于原始数据中的测量误差。如果矩形矩阵 A 没有线性无关的列,则该矩阵秩亏。如果 A 秩亏,则 AX = B 的最小二乘解不唯一。如果A 秩亏,则 A\B 会发出警告,并生成一个最小二乘解。您可以使用 lsqminnorm 求在所有解中具有最小范数的解 X。